题目内容
6. 如图,矩形ABCD中,AB=3,BC=10,点P是AD上的一个动点,若以A,P,B为顶点的三角形与△PDC相似,则AP=1或5或9.
如图,矩形ABCD中,AB=3,BC=10,点P是AD上的一个动点,若以A,P,B为顶点的三角形与△PDC相似,则AP=1或5或9.
分析 设AP=x,则PD=AD-AP=10-x,然后分类讨论:若∠APB=∠DPC,则Rt△APB∽Rt△DPC,得到比例式,代入求出即可;若∠APB=∠PCD,则Rt△APB∽Rt△DCP,得到比例式,代入求出即可.
解答 解:∵四边形ABCD是矩形,
∴AB=DC=3,AD=BC=10,∠A=∠D=90°,
设AP=x,则PD=AD-AP=10-x,
若∠APB=∠DPC,则Rt△APB∽Rt△DPC,
所以$\frac{AP}{PD}$=$\frac{AB}{CD}$,即$\frac{x}{10-x}$=$\frac{3}{3}$,
解得:x=5;
若∠APB=∠PCD,则Rt△APB∽Rt△DCP,
所以$\frac{AB}{DP}$=$\frac{AP}{CD}$,
$\frac{3}{10-x}$=$\frac{x}{3}$,
解得:x=1或9;
所以当AP=1或5或9时,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,即这样的P点有三个.
故答案为:1或5或9.
点评 本题考查了相似三角形的判定和判定,矩形的性质的应用,能求出符合的所有情况是解此题的关键,注意:有两组角对应相等的两个三角形相似,用了分类讨论的思想.

练习册系列答案
相关题目
17.一个直角三角形的面积是30,其两直角边的和是17,则其斜边长为( )
| A. | 17 | B. | 26 | C. | 30 | D. | 13 |
11.下列计算正确的是( )
| A. | $\sqrt{4}$-$\sqrt{3}$=1 | B. | $\sqrt{2}$×$\sqrt{\frac{1}{2}}$=1 | C. | $\sqrt{6}$÷$\sqrt{2}$=2 | D. | $\sqrt{8}$=±2$\sqrt{2}$ |
16.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
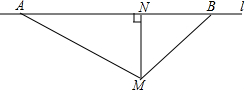 根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速60千米/时.已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离(即MN的长)为30米.现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.
根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速60千米/时.已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离(即MN的长)为30米.现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.