题目内容
2.已知点P是⊙O所在平面内一点,点P到⊙O上各点的最大距离为a,最小距离为b(a>b),则⊙O的半径为( )| A. | $\frac{a+b}{2}$ | B. | $\frac{a-b}{2}$ | C. | a-b或a+b | D. | $\frac{a-b}{2}$或$\frac{a+b}{2}$ |
分析 点P可能在圆内,也可能在圆外;当点P在圆内时,直径为最大距离与最小距离的和;当点P在圆外时,直径为最大距离与最小距离的差;再分别计算半径.
解答 解:若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b,
若这个点在圆的内部或在圆上时,圆的直径为a+b,因而半径为$\frac{a+b}{2}$;
当此点在圆外时,圆的直径是a-b,因而半径是$\frac{a-b}{2}$;
故选D.
点评 本题考查了点与圆的位置关系,培养学生分类的思想及对点P到圆上最大距离、最小距离的认识.

练习册系列答案
相关题目
11.已知实数a是方程x2-3x-2=0的其中一个根,则-2a2+6a+7等于( )
| A. | 11 | B. | 9 | C. | 7 | D. | 3 |
12.如表是二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的对应关系,一元二次方程ax2+bx+c=$\frac{3}{10}$(a≠0)的一个解x的取值范围是6.2<x<6.3.
| x | 6.1 | 6.2 | 6.3 | 6.4 |
| y=ax2+bx+c | -0.3 | -0.1 | 0.2 | 0.4 |
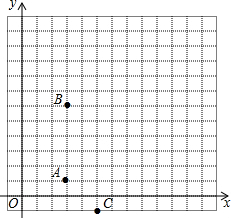 某城市的街道恰好呈东西与南北横纵交错格局(如图所示),一次,警察局电子监控器屏幕上发现一辆作案后的小轿车正在点A(3,1)处以每分钟0.5个单位长度的速度向北逃窜,根据各街道的交通状况进行分析,逃犯很可能逃到点B(3,6)后改为向东逃窜,此时正在点C(5,-1)处巡逻的警车接到指令后立即以每分钟0.7个单位长度的速度进行追捕,逃犯将在什么地方被追捕到?
某城市的街道恰好呈东西与南北横纵交错格局(如图所示),一次,警察局电子监控器屏幕上发现一辆作案后的小轿车正在点A(3,1)处以每分钟0.5个单位长度的速度向北逃窜,根据各街道的交通状况进行分析,逃犯很可能逃到点B(3,6)后改为向东逃窜,此时正在点C(5,-1)处巡逻的警车接到指令后立即以每分钟0.7个单位长度的速度进行追捕,逃犯将在什么地方被追捕到?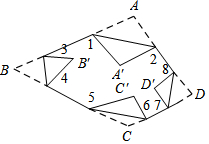 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.