题目内容
13.边长为a的正六边形的内切圆的半径为( )| A. | $\frac{\sqrt{3}}{2}$a | B. | $\frac{1}{2}$a | C. | 2a | D. | a |
分析 首先求出正多边形的内切圆的半径,即为每个边长为a的正三角形的高,从而构造直角三角形即可解.
解答 解:如图,连接OA、OB,OG;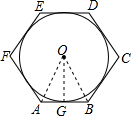
∵六边形ABCDEF是边长为a的正六边形,
∴△OAB是等边三角形,
∴OA=AB=a,
∴OG=OA•sin60°=$\frac{\sqrt{3}}{2}$a,
∴边长为a的正六边形的内切圆的半径为$\frac{\sqrt{3}}{2}$a,
故选A.
点评 本题涉及到正多边形、等边三角形及特殊角的三角函数值,作出图形,理解定义是解答此题的关键.

练习册系列答案
相关题目
3.以下图形中不是轴对称图形的是( )
| A. | 正方形 | B. | 等边三角形 | C. | 矩形 | D. | 平行四边形 |
1.到三角形三边距离相等的点是三角形三条( )的交点.
| A. | 高 | B. | 中线 | C. | 角平分线 | D. | 以上都正确 |
8.已知|a|=5,|b|=8,且a+b<0,则式子a-b的值为( )
| A. | 13 | B. | -13 | C. | 13或-13 | D. | 13或3 |
18. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且高于x的一元二次方程ax2+bx+m=0有实数根.有以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且高于x的一元二次方程ax2+bx+m=0有实数根.有以下结论:
①b2-4ac>0;②abc=0;③m的最大值为3.
其中,正确的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且高于x的一元二次方程ax2+bx+m=0有实数根.有以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且高于x的一元二次方程ax2+bx+m=0有实数根.有以下结论:①b2-4ac>0;②abc=0;③m的最大值为3.
其中,正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.在0.101001001,$\frac{1}{3}$,π,$\sqrt{5}$这四个数中,无理数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.若最简二次根式$\sqrt{2x+1}$和$\sqrt{4x-3}$能合并,则x的值是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |

 如图,要使?ABCD成为菱形,则需添加一个条件是BA=BC(答案不唯一).
如图,要使?ABCD成为菱形,则需添加一个条件是BA=BC(答案不唯一).