题目内容

20．如图，圆锥的侧面展开图是半径为4，圆心角为90°的扇形，则该圆锥的底面周长为（　　）
A．πB．2πC．8πD．16

分析 根据圆锥侧面展开扇形的弧长等于底面圆的周长，可以求出底面圆的半径，从而求得圆锥的底面周长．

解答 解：设底面圆的半径为r，则：
2πr=$\frac{90π×4}{180}$=2π．
解得r=1，
故圆锥的底面周长为2π×1=2π．
故选：B．

点评 本题考查的是弧长的计算，利用弧长公式求出弧长，然后根据扇形弧长与圆锥底面半径的关系求出底面圆的半径．

练习册系列答案
相关题目
10．下列关于分式的判断，正确的是（　　）
A．当x=2时，$\frac{x+1}{x-2}$的值为零
B．无论x为何有理数，$\frac{3}{{x}^{2}+1}$的值为正数
C．无论x为何值，$\frac{3}{x+1}$的值不可能为正数
D．当x≠3时，$\frac{x-3}{x}$有意义
11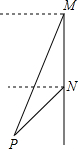．如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离是（　　）（结果精确到0.1海里）【参考数据：sin68°=0.9272，sin46°=0.7193，sin22°=0.3746，sin44°=0.6947】
A．22.5B．41.7C．43.1D．55.6
8．已知二次函数y=-x2+2x+c的图象上三个点的坐标分别为A（-2，y1），B（-1，y2），C（2，y3），则y1，y2，y3的大小关系为（　　）
A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y2＞y1D．y3＞y1＞y2
15．如图，一副三角板按图放置，则∠1的度数为（　　）
A．30°B．60°C．80°D．75°
5．下列说法正确的是（　　）
A．数据4、5、5、6、0的平均数是5
B．数据2、3、4、2、3的众数是2
C．了解某班同学的身高情况适合全面调查
D．甲、乙两组数据的平均数相同，方差分别是S甲2=3.2，S乙2=2.9，则甲组数据更稳定
12．如图，AD是△ABC是角平分线，E、F分别是边AB、AC的中点，连接DE、DF，要使四边形AEDF是菱形还需要添加一个条件，这个条件不可能是（　　）
A．AD⊥BCB．AB=ACC．AD=BCD．BD=DC
9．对于每个非零自然数n，抛物线$y={x^2}-\frac{2n+1}{{n（{n+1}）}}x+\frac{1}{{n（{n+1}）}}$与x轴交于An，Bn两点，以AnBn表示这两点间的距离，则A1B1+A2B2+…+A2016B2016的值是（　　）
A．$\frac{2016}{2015}$B．$\frac{2015}{2016}$C．$\frac{2017}{2016}$D．$\frac{2016}{2017}$
10．2017的绝对值是（　　）
A．2017B．-2017C．0D．$\frac{1}{2017}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网