题目内容
20. 解不等式组$\left\{\begin{array}{l}{x-4≥3(x-2)}\\{\frac{7x+11}{3}-1>-x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-4≥3(x-2)}\\{\frac{7x+11}{3}-1>-x}\end{array}\right.$,并把它的解集在数轴上表示出来.
分析 首先计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集,然后再在数轴上表示即可.
解答 解:$\left\{\begin{array}{l}{x-4≥3(x-2)①}\\{\frac{7x+11}{3}-1>-x②}\end{array}\right.$,
由①得:x≤1,
由②得:x>-$\frac{4}{5}$,
不等式组的解集为-$\frac{4}{5}$<x≤1,
在数轴上表示为: .
.
点评 此题主要考查了解一元一次不等式组,以及在数轴上表示不等式的解集,关键是掌握在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
10.cos60°•sin60°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
4.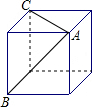 如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )
如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )
 如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )
如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC等于( )| A. | 60° | B. | 75° | C. | 90° | D. | 135° |
8. 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )| A. | (2,0) | B. | (3,0) | C. | (4,0) | D. | (5,0) |
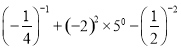
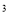 (y-x)
(y-x) 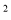 (x-y)+2(x-y)
(x-y)+2(x-y) 
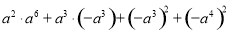
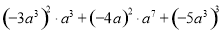
 把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:
把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论: 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来)
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来) 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=10.
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=10.