题目内容
15. 已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A、B两点,如图所示,其中A(-1,-1),
已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A、B两点,如图所示,其中A(-1,-1),(1)求二次函数和一次函数解析式.
(2)求△OAB的面积.
分析 (1)利用点A的坐标可求出直线与抛物线的解析式;
(2)求出点G的坐标及点B的坐标,利用S△OAB=$\frac{1}{2}$OG•|A的横坐标|+$\frac{1}{2}$OG•点B的横坐标求解即可.
解答 解:(1)∵一次函数y=kx-2的图象相过点A(-1,-1),
∴-1=-k-2,解得k=-1,
∴一次函数表达式为y=-x-2,
∵y=ax2过点A(-1,-1),
∴-1=a×1,解得a=-1,
∴二次函数表达式为y=-x2,
(2)在y=-x-2中,令x=0,得y=-2,
∴G(0,-2),
由一次函数与二次函数联立可得$\left\{\begin{array}{l}{y=-x-2}\\{y=-{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$
∴S△OAB=$\frac{1}{2}$OG•|A的横坐标|+$\frac{1}{2}$OG•点B的横坐标=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=1+2=3.
点评 本题主要考查了待定系数法求函数解析式,解题的关键是正确的求出点B的坐标.

练习册系列答案
相关题目
5.下列方程是一元二次方程的一般形式的是( )
| A. | (x-1)2=16 | B. | 3(x-2)2=27 | C. | 5x2-3x=0 | D. | $\sqrt{2}$x2+2x=8 |
3.已知α为锐角,关于x的方程3x2-4x•sinα+2(1-cosα)=0有两个不相等的实数根,α为锐角,那么α的取值范围是( )
| A. | 0°<α<30° | B. | 0°<α<60° | C. | 30°<α<60° | D. | 60°<α<90° |
20.下列方程中,关于x的一元二次方程是( )
| A. | x2+3x-5 | B. | 3x3-2x+5=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
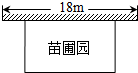 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.