题目内容
6.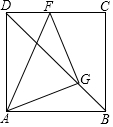 如图,边长为4的正方形ABCD,F是边DC上一点,射线AF顺时针旋转45°,交对角线BD于点G.
如图,边长为4的正方形ABCD,F是边DC上一点,射线AF顺时针旋转45°,交对角线BD于点G.(1)探究AG、FG的关系,并说明理由.
(2)设DF为x,四边形ADFG面积为y,求x、y的函数关系式.
分析 (1)先根据∠BAG=∠CAF,∠ABG=∠ACF=45°,判定△ABG∽△ACF,进而得出$\frac{AG}{AB}$=$\frac{AF}{AC}$,再根据∠GAF=∠BAC=45°,即可得到△AGF∽△ABC,据此可得AG、FG的关系;
(2)根据正方形ABCD的边长为4,DF=x,即可得到AF2=42+x2=16+x2,再根据S四边形ADFG=S△ADF+S△AFG,进行计算即可得到x、y的函数关系式.
解答 解:(1)如图,连接AC,则∠BAC=∠∠GAF=45°,
∴∠BAG=∠CAF,
又∵∠ABG=∠ACF=45°,
∴△ABG∽△ACF,
∴$\frac{AG}{AF}$=$\frac{AB}{AC}$,即$\frac{AG}{AB}$=$\frac{AF}{AC}$,
又∵∠GAF=∠BAC=45°,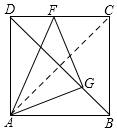
∴△AGF∽△ABC,
∵△ABC是等腰直角三角形,
∴△AGF是等腰直角三角形,
∵AB=BC,
∴AG=FG;
(2)∵正方形ABCD的边长为4,DF=x,
∴AF2=42+x2=16+x2,
∵S四边形ADFG=S△ADF+S△AFG,
∴y=$\frac{1}{2}$×4×x+$\frac{1}{4}$(16+x2)=$\frac{1}{4}{x}^{2}$+2x+4(0<x≤4).
点评 本题主要考查了相似三角形的判定与性质,正方形的性质的综合应用,解决问题的关键是作辅助线构造相似三角形,依据相似三角形的对应边成比例解决问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
16.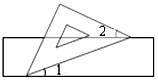 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )| A. | 20o | B. | 25o | C. | 30o | D. | 15o |
17.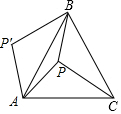 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )| A. | 4$\sqrt{3}$+6 | B. | 12$\sqrt{3}$+6 | C. | 60 | D. | 42 |
14.已知一元二次方程x2-3x+4=0的两根x1、x2,则x1+x2=( )
| A. | 4 | B. | 3 | C. | -4 | D. | -3 |
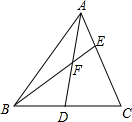 已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$.
已知如图,F为AD的中点,$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{BD}{CD}$和$\frac{BF}{FE}$. 如图,AC是?ABCD的对角线,以点C为圆心,CD长为半径作圆弧,交AC与点E,连结DE并延长交AB于点F,求证:AF=AE.
如图,AC是?ABCD的对角线,以点C为圆心,CD长为半径作圆弧,交AC与点E,连结DE并延长交AB于点F,求证:AF=AE.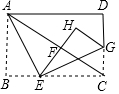 如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.
如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.