题目内容
3.已知抛物线y=k(x-1)(x-$\frac{3}{k}$)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 整理抛物线解析式,确定出抛物线与x轴的一个交点A和y轴的交点C,然后求出AC的长度,再分:
①k>0时,点B在x轴正半轴时,分AC=BC、AC=AB、AB=BC三种情况求解;
②k<0时,点B在x轴的负半轴时,点B只能在点A的左边,只有AC=AB一种情况列式计算即可.
解答 解:y=k(x-1)(x-$\frac{3}{k}$)=(x-1)(kx-3),
所以,抛物线经过点A(1,0),C(0,3),
AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{10}$,
点B坐标为($\frac{3}{k}$,0),
①k>0时,点B在x正半轴上,
若AC=BC,则$\sqrt{(\frac{3}{k})^{2}+{3}^{2}}$=$\sqrt{10}$,解得k=3,
若AC=AB,则$\frac{3}{k}$-1=$\sqrt{10}$,解得k=$\frac{\sqrt{10}-1}{3}$,
若AB=BC,则$\frac{3}{k}$-1=$\sqrt{(\frac{3}{k})^{2}+{3}^{2}}$,解得k=-$\frac{3}{4}$;不合题意,舍去;
②k<0时,点B在x轴的负半轴,点B只能在点A的左侧,
只有AC=AB,则1-$\frac{3}{k}$=$\sqrt{10}$,解得k=-$\frac{\sqrt{10}+1}{3}$,
所以,能使△ABC为等腰三角形的抛物线共有3条.
故选:B.
点评 本题考查了抛物线与x轴的交点问题,根据抛物线的解析式确定出抛物线经过的两个定点是解题的关键,注意分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.收入8元,又支出5元,可用算式表示为( )
| A. | (+8)+(+5) | B. | (+8)+(-5) | C. | (-8)+(-5) | D. | (-8)+(+5) |
 ,则
,则 的值是( )
的值是( ) B. -
B. - C.
C.  D.
D. 
 的解满足x+y=﹣2,求k的值.
的解满足x+y=﹣2,求k的值.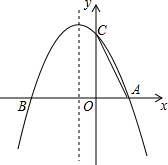 如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.