Question

12．已知抛物线y=-x²+4x-3与x轴交于A、B两点，顶点为C．
（1）求A、B、C三点的坐标；
（2）根据图象说明：
①当x取何值时，y=0？
②当x取何值时，y＞0？
③当x取何值时，y＜0？
④写出y随x的增大而减小的自变量x的取值范围．

Answer 1

分析 （1）令y=0可得A、B两点坐标，由（-$\frac{b}{2a}$，$\frac{4ac{-b}^{2}}{4a}$）可得顶点坐标C；
（2）根据图象可得结果．

解答 解：（1）令y=0，则-x²+4x-3=0，解得：x=3或x=1，
∴A，B两点坐标分别为（3，0）或（1，0），
由（-$\frac{b}{2a}$，$\frac{4ac{-b}^{2}}{4a}$）可得顶点坐标C为（2，3）；

（2）图象如图所示：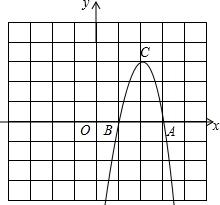

①当x=1或3时，y=0；
②当1＜x＜3时，y＞0；
③当x＜1或x＞3时，y＜0；
④y随x的增大而减小的自变量x的取值范围时x＜2．

点评 本题考查了二次函数的图象与x轴的交点和二次函数的性质以及函数图象上点的坐标特征，根据坐标特征确定交点坐标和顶点坐标是解题的关键．