题目内容
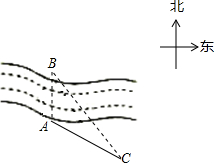 在一次测量活动中,同学们想测量河岸上的树A与它对岸正北方向的树B之间的距离,如图,他们在河岸边上选择了与树A及树B在同一水平面上的点C的北偏西35°方向,树A位于点C的北偏西58°方向,又测得A、C间的距离为100m,请你利用以上测得的数据求出树A 树B之间的距离.(结果精确到1米,参考数据sin23°≈0.391,sin35°≈0.574,tan35°≈0.700,sin58°≈0.848,cos58°≈0.530.)
在一次测量活动中,同学们想测量河岸上的树A与它对岸正北方向的树B之间的距离,如图,他们在河岸边上选择了与树A及树B在同一水平面上的点C的北偏西35°方向,树A位于点C的北偏西58°方向,又测得A、C间的距离为100m,请你利用以上测得的数据求出树A 树B之间的距离.(结果精确到1米,参考数据sin23°≈0.391,sin35°≈0.574,tan35°≈0.700,sin58°≈0.848,cos58°≈0.530.)考点:解直角三角形的应用-方向角问题
专题:
分析:过点A作AH垂直BC,垂足为点H,在Rt△ACH中求出AH的长,再在Rt△ABH中,求出AB的长.
解答: 解:过点A作AH垂直BC,垂足为点H,
解:过点A作AH垂直BC,垂足为点H,
由题意,得∠B=35°,
∠C=58°-35°=23°,
在Rt△ACH中,
AH=AC•sinC=100×sin23°≈39.1,
在Rt△ABH中,AB=
≈
≈68米.
答:树A与树B之间的距离约为68米.
 解:过点A作AH垂直BC,垂足为点H,
解:过点A作AH垂直BC,垂足为点H,由题意,得∠B=35°,
∠C=58°-35°=23°,
在Rt△ACH中,
AH=AC•sinC=100×sin23°≈39.1,
在Rt△ABH中,AB=
| AH |
| sinB |
| 39.1 |
| sin35° |
答:树A与树B之间的距离约为68米.
点评:本题考查了解直角三角形的应用--方向角问题,结合测量问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,每个小正方形的边长均为a,则阴影部分的面积为( )
如图,每个小正方形的边长均为a,则阴影部分的面积为( )| A、5a2 | ||
| B、4a2 | ||
| C、3a2 | ||
D、
|
已知等腰三角形ABC的两个顶点坐标为A(0,2
),B(2,0),第三个顶点C在坐标轴上,则满足条件的点C的个数是( )
| 3 |
| A、5个 | B、6个 | C、7个 | D、8个 |
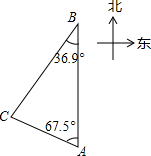 某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?
某国汉阳石油运输船在临近我国海域发生原油泄漏事故,我国国家海洋局紧急调集海上巡逻的海监船,在相关海域进行现场监测与海洋采样,如图,上午9时,海监船位于A处,观测到某还港口城市P位于海监船的北偏西67.5°方向,海监船以21海里/时的速度向正北方向行驶,下午2时海监船到达B处,这时观察到城市P位于海监船的南偏西36.9°,求此时海监船所在B处于城市P的距离?