题目内容
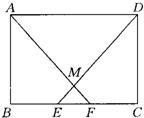45、如图所示，在矩形ABCD中，点E，F在BC边上，且BE=CF，AF，DE相交于点M，求证：AM=DM．
分析：易证得△ABF≌△DCE，可得到∠AFB=∠DEC，利用矩形的对边平行的性质可求得它们的内错角也是相等的，进而得到AM=DM．
解答：证明：∵四边形ABCD为矩形，
∴∠B=∠C=90°，AD∥BC，AB=DC．
∵BE=CF，
∴BF=CE．
∴△ABF≌△DCE（SAS）．
∴∠AFB=∠DEC．
∵AD∥BC，
∴∠AFB=∠DAF，∠DEC=∠ADE．
∴∠FAD=∠EDA．
∴AM=DM．
∴∠B=∠C=90°，AD∥BC，AB=DC．
∵BE=CF，
∴BF=CE．
∴△ABF≌△DCE（SAS）．
∴∠AFB=∠DEC．
∵AD∥BC，
∴∠AFB=∠DAF，∠DEC=∠ADE．
∴∠FAD=∠EDA．
∴AM=DM．
点评：应用的知识点为：矩形的对边平行；全等三角形的对应角相等，等角对等边等知识的综合运用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
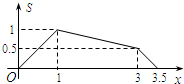
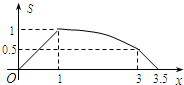
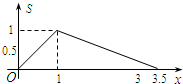
如图所示，在矩形ABCD中，AB=1，BC=2，E是CD边的中点．点P从点A开始，沿逆时针方向在矩形边上匀速运动，到点E停止．设点P经过的路程为x，△APE的面积为S，则S关于x的函数关系的大致图象是（ ）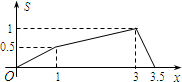
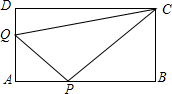P也随之停止运动．用t表示移动时间，设四边形QAPC的面积为S．
B=nBC
如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C运动，点P、Q的速度都是1cm/s．