题目内容
20.用适当的方法解方程:(1)x2-1=x;
(2)(2y-1)2=3(1-2y);
(3)3x2-8x-3=0.
分析 (1)利用配方得到完全平方形式再解方程;
(2)利用提取公因式法对方程进行化简,再解方程即可;
(3)利用十字相乘法化简方程,再接方程即可.
解答 解:(1)x2-1=x,
移项,得x2-x-1=0,
配方,得x2-x+$\frac{1}{4}$=$\frac{5}{4}$,
即:${(x-\frac{1}{2})}^{2}$=$\frac{5}{4}$,
解得x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
(2)(2y-1)2=3(1-2y),
移项,得(2y-1)2+3(2y-1),
提取公因式,得(2y-1)(2y-1+3)=0,
解得:y1=$\frac{1}{2}$,y2=-1.
(3)3x2-8x-3=0,
分解因式,得(3x+1)(x-3)=0,
解得:x1=3,x2=-$\frac{1}{3}$.
点评 本题考查一元一次方程的解法,分别用到了配方法、提取公因式法和十字相乘法,解题的关键是会用分解因式的方法解方程.

练习册系列答案
相关题目
11.某商场举行投资促销活动,对于“抽到一等奖的概率为$\frac{1}{10}$”,下列说法正确的是( )
| A. | 抽一次不可能抽到一等奖 | |
| B. | 抽10次也可能没有抽到一等奖 | |
| C. | 抽10次奖必有一次抽到一等奖 | |
| D. | 抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖 |
 如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为40cm2.
如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为40cm2.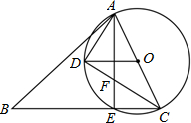 如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.