Question

4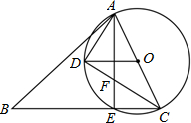．如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，$\frac{1}{2}$AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．
（1）求证：D是$\widehat{AE}$的中点；
（2）求证：∠DAO=∠B+∠BAD．

Answer 1

分析 （1）根据圆同弧或等弧所对的圆周角相等，可以证明该结论；
（2）根据OD∥BC，OD=OA，可以得到角的关系，然后通过转化就可以证明结论．

解答 （1）∵由已知可得，OD∥BC，OD=OC，
∴∠ODC=∠DCE，∠ODC=∠OCD，
∴∠OCD=∠DCE，
∴弧AD=弧DE，
即D是$\widehat{AE}$的中点；
（2）证明：延长AD与BC交于点G，如下图所示，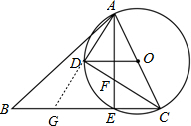

∵OD∥BC，OD=OA，
∴∠ADO=∠AGE，∠ADO=∠DAO，
∴∠AGE=∠DAO，
∵∠AGE=∠B+∠BAD，
∴∠DAO=∠B+∠BAD．

点评 本题考查圆周角定理，圆心角、弧、弦的关系、平行线的性质，三角形的外角与内角的关系，解题的关键是明确题意，找出所求结论需要的条件．