题目内容
1.先化简,后求值:$\frac{x-4}{x}$÷($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$),其中x=$\sqrt{2}$+2.分析 先将原式化简,再将x的值代入即可求出答案.
解答 解:当x=$\sqrt{2}$+2
原式=$\frac{x-4}{x}$÷[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]
=$\frac{x-4}{x}$÷$\frac{x-4}{x(x-2)^{2}}$
=(x-2)2
=($\sqrt{2}$)2
=2
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
9.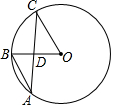 如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )
如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )
 如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )
如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )| A. | 81° | B. | 72° | C. | 60° | D. | 63° |
16.π是$\frac{1}{π}$的( )
| A. | 绝对值 | B. | 倒数 | C. | 相反数 | D. | 平方根 |
 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(1,3),B(-3,m).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(1,3),B(-3,m).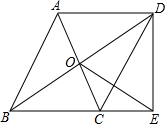 如图,?ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
如图,?ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.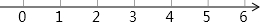
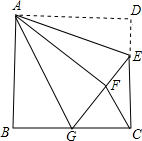 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.
如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.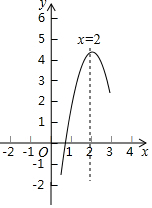 如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)
如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)