题目内容
8.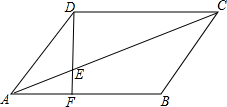 如图,在平行四边形ABCD中,点E在AC三分一处,即AE=$\frac{1}{3}$AC,DE的延长线交AB于点F,猜想:AF与FB的数量关系,并证明.
如图,在平行四边形ABCD中,点E在AC三分一处,即AE=$\frac{1}{3}$AC,DE的延长线交AB于点F,猜想:AF与FB的数量关系,并证明.
分析 根据平行四边形的性质得出AB=CD,AB∥CD,根据相似三角形的判定推出△AEF∽△CED,得出比例式,代入求出即可.
解答 解:AF=FB,
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CED,
∴$\frac{AE}{CE}=\frac{AF}{DC}$,
∵AE=$\frac{1}{3}$AC,∴CE=2AE,
∴$\frac{AF}{AB}=\frac{1}{2}$,
∵AF+BF=AB,
∴AF=FB.
点评 本题考查了平行四边饿形的性质,相似三角形的性质和判定的应用,解此题的关键是推出△AEF∽△CED.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | -0.064的立方根是0.4 | |
| B. | 一个数的平方根与它的立方根相等,则这个数是0 | |
| C. | -9的平方根是±3 | |
| D. | -7是(-7)2的算术平方根 |
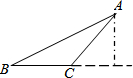 如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.
如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.