题目内容
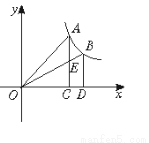
如图,过反比例函数y=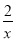 (x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .
(x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .
S1=S2.
【解析】
试题分析:易得△AOC和△OBD的面积相等,都减去公共部分△OCE的面积可得S1、S2的大小关系.
试题解析:设点A的坐标为(x,y),点B的坐标为(a,b),
∵A、B在反比例函数y= 上,
上,
∴xy=2,ab=2,
∴S△AOC= xy=1;S△OBD=
xy=1;S△OBD= ab=1.
ab=1.
∴S△AOC=S△OBD,
∴S△AOC-S△OCE=S△OBD-S△OCE,
即S1=S2.
故选C.
考点:反比例函数系数k的几何意义.

练习册系列答案
相关题目

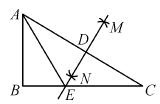
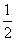 AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.