题目内容
△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论不正确的是( )
| A、c•sinA=a |
| B、c•cosB=b |
| C、b•tanA=a |
| D、a•tanB=b |
考点:锐角三角函数的定义,勾股定理的逆定理
专题:
分析:根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,可得答案.
解答:解:由a2+b2=c2,得∠C=90°,
A、sin A=
,故A正确;
B、cos=
,故B错误;
C、tanA=
,故C正确;
D、tanB=
,故D正确;
故选:B.
A、sin A=
| a |
| c |
B、cos=
| a |
| c |
C、tanA=
| a |
| b |
D、tanB=
| b |
| a |
故选:B.
点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
 图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )| A、体育场离张强家2.5千米 |
| B、体育场离早餐店4千米 |
| C、张强在体育场锻炼了15分钟 |
| D、张强从早餐店回家的平均速度是3千米/小时 |
数轴上的点A到原点的距离是8,则点A表示的数为( )
| A、8 | B、4或-4 |
| C、8或-8 | D、4 |
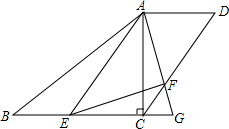 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.



 如图,是两块边长分别为a、b的黑色正方形瓷砖和两块白色的长方形瓷砖拼成的无缝图案.
如图,是两块边长分别为a、b的黑色正方形瓷砖和两块白色的长方形瓷砖拼成的无缝图案.