题目内容
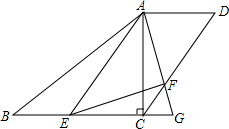 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=x.(1)使用x的代数式表示FC;
(2)设
| FG |
| EF |
(3)当△AEG是等腰三角形时,直线写出BE的长.
考点:相似形综合题
专题:综合题,分类讨论,转化思想
分析:(1)易证△ABC∽△DCA,则有∠B=∠ACD,由∠EAF=∠BAC可得∠BAE=∠CAF,从而得到△ABE∽△ACF,然后根据相似三角形的性质即可解决问题;
(2))由△ABE∽△ACF可得
=
,根据∠EAF=∠BAC可得△AEF∽△ABC,从而得到EF=
AF.易证△CFG∽△DFA,从而得到
=
,问题得以解决;
(3)易证△ADF∽△GAE,因而当△GAE是等腰三角形时,△ADF也是等腰三角形,然后只需分三种情况(①AF=DF,②AD=DF,③AF=AD,)讨论,就可解决问题.
(2))由△ABE∽△ACF可得
| AB |
| AC |
| AE |
| AF |
| 4 |
| 3 |
| FG |
| FA |
| CF |
| DF |
(3)易证△ADF∽△GAE,因而当△GAE是等腰三角形时,△ADF也是等腰三角形,然后只需分三种情况(①AF=DF,②AD=DF,③AF=AD,)讨论,就可解决问题.
解答:解:(1)如图1,
∵AC⊥BC,∴∠ACB=90°.
∵AD∥BC,∴∠DAC=∠ACB=90°.
∵AD=9,AC=12,BC=16,
∴AB=20,DC=15.
∵
=
=
,∠DAC=∠ACB,
∴△ABC∽△DCA,
∴∠B=∠ACD.
∵∠EAF=∠BAC,
∴∠BAE=∠CAF,
∴△ABE∽△ACF,
∴
=
,
∴
=
,
∴CF=
x;
(2)∵△ABE∽△ACF,
∴
=
,
又∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴
=
=
=
,
∴EF=
AF.
∵AD∥CG,
∴△CFG∽△DFA,
∴
=
,
∴y=
=
=
•
=
•
,
整理得:y=
(0<x≤16);
(3)当△AEG是等腰三角形时,BE的长为
、10或7.
解题过程如下:
∵△ABC∽△DCA,∴∠BAC=∠D,
∴∠EAF=∠BAC=∠D.
∵AD∥BC,∴∠G=∠FAD,
∴△ADF∽△GAE,
∴当△GAE是等腰三角形时,△ADF也是等腰三角形.
①当AF=DF时,
则有∠FAD=∠D,
∵∠FAD+∠CAF=90°,∠D+∠ACD=90°,
∴∠CAF=∠ACD,
∴FA=FC,
∴CF=DF=
,
∴
x=
,
∴x=
;
②当AD=DF=9时,CF=CD-DF=6,
∴
x=6,
∴x=10;
③当AF=AD=9时,
作AH⊥DF于H,如图2,
则有DH=FH.
∵S△CAD=
AC•AD=
CD•AH,
∴AH=
=
,
∴FH=DH=
=
,
∴
x=15-2×
,
∴x=7.
∵AC⊥BC,∴∠ACB=90°.
∵AD∥BC,∴∠DAC=∠ACB=90°.
∵AD=9,AC=12,BC=16,
∴AB=20,DC=15.
∵
| BC |
| AC |
| AC |
| AD |
| 4 |
| 3 |
∴△ABC∽△DCA,
∴∠B=∠ACD.
∵∠EAF=∠BAC,
∴∠BAE=∠CAF,

∴△ABE∽△ACF,
∴
| AB |
| AC |
| BE |
| CF |
∴
| 20 |
| 12 |
| x |
| CF |
∴CF=
| 3 |
| 5 |
(2)∵△ABE∽△ACF,
∴
| AB |
| AC |
| AE |
| AF |
又∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴
| EF |
| AF |
| BC |
| AC |
| 16 |
| 12 |
| 4 |
| 3 |
∴EF=
| 4 |
| 3 |
∵AD∥CG,
∴△CFG∽△DFA,
∴
| FG |
| FA |
| CF |
| DF |
∴y=
| FG |
| EF |
| FG | ||
|
| 3 |
| 4 |
| CF |
| DF |
| 3 |
| 4 |
| ||
15-
|
整理得:y=
| 3x |
| 100-4x |
(3)当△AEG是等腰三角形时,BE的长为
| 25 |
| 2 |
解题过程如下:
∵△ABC∽△DCA,∴∠BAC=∠D,
∴∠EAF=∠BAC=∠D.
∵AD∥BC,∴∠G=∠FAD,
∴△ADF∽△GAE,
∴当△GAE是等腰三角形时,△ADF也是等腰三角形.
①当AF=DF时,
则有∠FAD=∠D,
∵∠FAD+∠CAF=90°,∠D+∠ACD=90°,
∴∠CAF=∠ACD,
∴FA=FC,
∴CF=DF=
| 15 |
| 2 |
∴
| 3 |
| 5 |
| 15 |
| 2 |

∴x=
| 25 |
| 2 |
②当AD=DF=9时,CF=CD-DF=6,
∴
| 3 |
| 5 |
∴x=10;
③当AF=AD=9时,
作AH⊥DF于H,如图2,
则有DH=FH.
∵S△CAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AH=
| AC•AD |
| CD |
| 36 |
| 5 |
∴FH=DH=
| AD2-AH2 |
| 27 |
| 5 |
∴
| 3 |
| 5 |
| 27 |
| 5 |
∴x=7.
点评:本题主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,在解决问题的过程中用到了面积法、分类讨论的思想,有一定的难度,证到△ABE∽△ACF是解决第(1)小题的关键,证到△AEF∽△ABC,从而得到EF=
AF是解决第(2)小题的关键,证到△ADF∽△GAE,从而把△GAE是等腰三角形转化为△ADF是等腰三角形是解决第(2)小题的关键.
| 4 |
| 3 |

练习册系列答案
相关题目
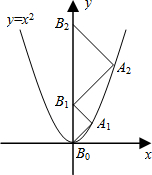 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )| A、2013 | ||
| B、2014 | ||
C、2013
| ||
D、2014
|
下列方程变形中,正确的是( )
| A、方程3x-2=2x+1,移项,得3x-2x=-1+2 | ||||
| B、方程6-x=2-5(x-2),去括号,得6-x=2-5x-2 | ||||
C、方程
| ||||
D、方程
|
下列方程中,解为x=3的方程是( )
| A、6x=2 | ||
| B、5x-15=0 | ||
C、
| ||
| D、3x+9=0 |
△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论不正确的是( )
| A、c•sinA=a |
| B、c•cosB=b |
| C、b•tanA=a |
| D、a•tanB=b |
 已知:如图,等边△ABC中,D为AC的中点,DG∥BG交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于F点.
已知:如图,等边△ABC中,D为AC的中点,DG∥BG交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于F点. 将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD=
将纸条照如图方式折一下,经测量∠ABC为30°,那么∠CBD=