题目内容
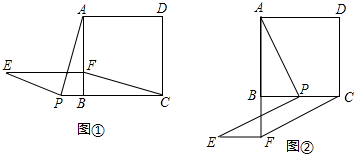
13.如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
分析 (1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论;
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠PBA=90°
在△PBA和△FBC中,
$\left\{\begin{array}{l}{AB=BC}\\{∠PBA=∠ABC}\\{BP=BF}\end{array}\right.$,
∴△PBA≌△FBC(SAS),
∴PA=FC,∠PAB=∠FCB.
∵PA=PE,
∴PE=FC.
∵∠PAB+∠APB=90°,
∴∠FCB+∠APB=90°.
∵∠EPA=90°,
∴∠APB+∠EPA+∠FCP=180°,
即∠EPC+∠PCF=180°,
∴EP∥FC,
∴四边形EPCF是平行四边形;
(2)解:结论:四边形EPCF是平行四边形,
理由是:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠CBF=90°
在△PBA和△FBC中,
$\left\{\begin{array}{l}{AB=BC}\\{∠PBA=∠ABC}\\{BP=BF}\end{array}\right.$,
∴△PBA≌△FBC(SAS),
∴PA=FC,∠PAB=∠FCB.
∵PA=PE,
∴PE=FC.
∵∠FCB+∠BFC=90°,
∠EPB+∠APB=90°,
∴∠BPE=∠FCB,
∴EP∥FC,
∴四边形EPCF是平行四边形.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,平行四边形的判定及性质的运用,解答时灵活运用平行四边形的判定方法是关键.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小明家2015年2月份用水20吨,交水费66元;3月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费为每吨3.3元?
 如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )
如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )| A. | 35° | B. | 50° | C. | 65° | D. | 85° |
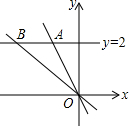 如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.
如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.

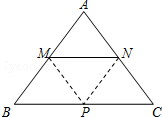 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.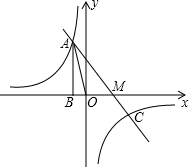 如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2). 如图,围棋盘的左下角呈现的是2015年3月7日韩国新人王战决赛第一局中的几手棋,为记录棋谱方便,横线用数字表示,竖线用英文字母表示,这样,黑棋①的位置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为(D,6).
如图,围棋盘的左下角呈现的是2015年3月7日韩国新人王战决赛第一局中的几手棋,为记录棋谱方便,横线用数字表示,竖线用英文字母表示,这样,黑棋①的位置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为(D,6).