题目内容
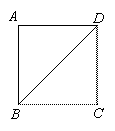
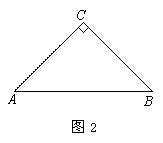
如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度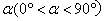 ,使点A,D,E在同一直线上,连接AD,BE.
,使点A,D,E在同一直线上,连接AD,BE.
(1) ① 依题意补全图2;
② 求证:AD=BE,且AD⊥BE;
③ 作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
 (2) 如图3,正方形ABCD边长为
(2) 如图3,正方形ABCD边长为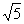 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
 |  | ||||
| |||||
(1) ① 依题意补全图2如图; ……………………………………1分
 ② 证明:∵∠ACB=∠DCE=90°,
② 证明:∵∠ACB=∠DCE=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE. ……………………………………2分
又∵CA=CB,CD=CE,
∴△ACD≌△BCE,
∴AD=BE, ……………………………………3分
∠CBE=∠CAD.
设AE与BC交于点F,则∠BFE=∠AFC,
∵∠AEB=180°-∠CBE-∠BFE,
∠ACB=180°-∠CAD-∠AFC,
∴∠AEB=∠ACB=90°,
即AD⊥BE. ……………………………………4分
③ 线段CM,AE,BE之间的数量关系:AE-BE=2CM.…………………5分
(2) 点A到BP的距离为1或2. ……………………………………7分

 阅读快车系列答案
阅读快车系列答案阅读下面材料:
在数学课上,老师提出如下问题:
|

小芸的作法如下:
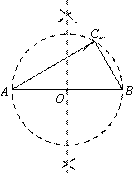
|
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是 .

 的一个同类项: .
的一个同类项: . 如图, C是线段AB外一点,按要求画图:
如图, C是线段AB外一点,按要求画图: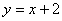 的图象与反比例函数
的图象与反比例函数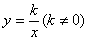 的图象交于A,B两点,且点A的坐标为(1,m).
的图象交于A,B两点,且点A的坐标为(1,m).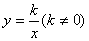 的表达式;
的表达式;
 是关于x的方程4x+m=3的解,那么m的值是
是关于x的方程4x+m=3的解,那么m的值是 C.-1 D.
C.-1 D. 
 的系数是 ,次数是 .
的系数是 ,次数是 . 写完后,让王红同学顺便给出一组a、b的值,老师自己说答案,当王红说完:“a=38,b=-32”后,李老师不假思索,立刻就说出答案“3”.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?请你通过计算说出其中的道理.
写完后,让王红同学顺便给出一组a、b的值,老师自己说答案,当王红说完:“a=38,b=-32”后,李老师不假思索,立刻就说出答案“3”.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?请你通过计算说出其中的道理.