题目内容
5.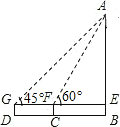 如图,初三年级某同学要测量校园内的旗杆AB的高度.在地面上C点用测角仪测得旗杆顶A点的仰角为∠AFE=60°,再沿着直线BC后退8米到D,在D点又测得旗杆顶A的仰角∠AGE=45°.已知测角仪DG的高度为1.6米,求旗杆AB的高度.($\sqrt{3}$的近似值取1.7,结果保留1位小数)
如图,初三年级某同学要测量校园内的旗杆AB的高度.在地面上C点用测角仪测得旗杆顶A点的仰角为∠AFE=60°,再沿着直线BC后退8米到D,在D点又测得旗杆顶A的仰角∠AGE=45°.已知测角仪DG的高度为1.6米,求旗杆AB的高度.($\sqrt{3}$的近似值取1.7,结果保留1位小数)
分析 设EF为x米,根据正切的概念求出AE,根据题意列出方程,解方程即可.
解答 解:设EF为x米,
在Rt△AEF中,∠AFE=60°,
∴AE=EF•tan60°=$\sqrt{3}$x,
在Rt△AGE中,∠AGE=45°,
∴AE=GE•tan45°=GE=8+x,
∴$\sqrt{3}$x=8+x,
解之,得x=4+4$\sqrt{3}$,
∴AE=GE=8+x=12+4$\sqrt{3}$≈18.8,
∴AB=18.8+1.6=20.4(米),
答:旗杆AB高20.4米.
点评 本题考查的是解直角三角形的应用-掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
20. 2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
 2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.
2016年6月20日,新一期全球超级计算机500强榜单公布,使用中国自主芯片制造的“神威太湖之光”取代“天河二号”登上榜首,中国超算上榜总数量也有史以来首次超过美国名列第一.据国际TOP500组织当天发布的榜单,“神威太湖之光”的浮点运算速度为每秒930000000亿次,不仅速度比第二名“天河二号”快出近两倍,其效率也提高3倍.930000000亿次用科学记数法可表示为( )亿次.| A. | 9.3×108 | B. | 9.3×107 | C. | 93×107 | D. | 0.93×109 |
10. 如图,已知AB∥CD,∠A=70°,则∠1度数是( )
如图,已知AB∥CD,∠A=70°,则∠1度数是( )
 如图,已知AB∥CD,∠A=70°,则∠1度数是( )
如图,已知AB∥CD,∠A=70°,则∠1度数是( )| A. | 70° | B. | 110° | C. | 100° | D. | 130° |
17.当x满足( )时,$\frac{\sqrt{1+x}}{x}$在实数范围内有意义.
| A. | x>-1 | B. | x≥1且x≠0 | C. | x≥-1 | D. | x≥-1且x≠0 |
 如图,是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在这个位置小正方体的个数,请分别画出从正面、左面看到的这个几何体的形状图.
如图,是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在这个位置小正方体的个数,请分别画出从正面、左面看到的这个几何体的形状图. 在数轴上表示a、b两数的点如图所示,用“>”或“<”填空:
在数轴上表示a、b两数的点如图所示,用“>”或“<”填空: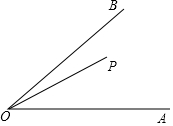 如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,则△PQR周长的最小值为10$\sqrt{2}$.