题目内容
12.计算(1)($\sqrt{3}$-$\sqrt{2}$)2+($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)
(2)$\sqrt{12}$×$\frac{{\sqrt{32}}}{3}$÷$\frac{{\sqrt{3}}}{3}$.
分析 (1)利用完全平方公式和平方差公式计算;
(2)先把二次根式化为最简二次根式,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=3-2$\sqrt{6}$+2+3-2
=6-2$\sqrt{6}$;
(2)原式=2$\sqrt{3}$×$\frac{4\sqrt{2}}{3}$×$\frac{3}{\sqrt{3}}$
=8$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a+2b=3ab | B. | 3a2-2a2=1 | C. | a6÷a2=a4 | D. | a2•a4=a8 |
20.某校举行书法比赛,为奖励优胜学生,购买了一些钢笔和毛笔,钢笔单价是毛笔单价的1.6倍,购买钢笔用了1200元,购买毛笔用1500元,购买的钢笔支数比毛笔少20支,钢笔、毛笔的单价分别是多少元?如果设毛笔的单价为x元/支,那么下面所列方程正确的是( )
| A. | $\frac{1200}{1.6x}$-$\frac{1500}{x}$=20 | B. | $\frac{1500}{x}$-$\frac{1200}{1.6x}$=20 | ||
| C. | $\frac{1500}{x}$=$\frac{1200}{1.6x}$-20 | D. | $\frac{1200}{x}$-$\frac{1500}{1.6x}$=20 |
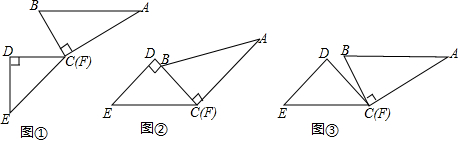
7. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )
如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )
 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )
如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.在平面直角坐标系中,点P(6,-10)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.设a>b,则下列各式中不能成立的是( )
| A. | a+3>b+3 | B. | a-4>b-4 | C. | 2a>2b | D. | -$\frac{a}{2}$>-$\frac{b}{2}$ |
16.某校学生会为了了解本校2000名学生的上学方式,采用问卷的方式对一部分学生进行了调查,在确定调查对象时,大家提出了两种方案:(A)在全校随机抽取150名学生进行调查.(B)在七年级随机抽取150名学生进行调查,学生会选择了其中的一种正确的调查方案,在问卷调查时,每位被调查时,每位被调查的学生都选择了问卷中的一种上学方式,学生会将收集到的数据进行整理,绘制成如下的统计表.
某校150名学生上学方式统计表
(1)学生会在确定调查对象时选择的正确方案是A(填“A”或“B”).
(2)根据抽样调查的结果,将估计出的全校2000名上学方式的情况绘制成合适的统计图(绘制一种即可)
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议,如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化建议.
某校150名学生上学方式统计表
| 方式 | 划记 | 频数 |
| 步行 |  | 15 |
| 骑车 |  | 51 |
| 乘公共交通工具 |  | 45 |
| 乘私家车 | 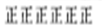 | 30 |
| 其他 | 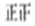 | 9 |
| 合计 | 150 |
(2)根据抽样调查的结果,将估计出的全校2000名上学方式的情况绘制成合适的统计图(绘制一种即可)
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议,如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化建议.