题目内容
10.图1为长方形纸片ABCD,AD=26,AB=22,直线L、M皆为长方形的对称轴.今将长方形纸片沿着L对折后,再沿着M对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI,如图2.最后将图2的五边形展开后形成一个八边形,如图2,且八边形的每一边长恰好均相等.(1)若图2中HI长度为x,请以x分别表示剪下的直角三角形的勾长和股长.
(2)请求出图3中八边形的一边长的数值,并写出完整的解题过程.
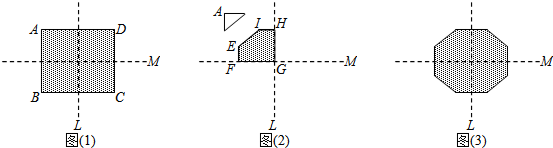
分析 (1)延长HI与FE相交于点N,根据折叠的性质找出HN、NF的长,再根据边与边之间的关系即可求出NI、NE的长度,由此即可得出剪下的直角三角形的勾长与股长;
(2)结合(1)的结论利用勾股定理得出线段EI的长,再根据正八边形的性质即可列出关于x的方程,解方程即可得出结论.
解答 解:(1)延长HI与FE相交于点N,如图所示.
∵HN=$\frac{1}{2}$AD=13,NF=$\frac{1}{2}$AB=11,HI=EF=x,
∴NI=HN-HI=13-x,NE=NF-EF=11-x,
∴剪下的直角三角形的勾长为11-x,股长为13-x.
(2)在Rt△ENI中,NI=13-x,NE=11-x,
∴EI=$\sqrt{N{I}^{2}+N{E}^{2}}$=$\sqrt{2{x}^{2}-48x+290}$.
∵八边形的每一边长恰好均相等,
∴EI=2HI=2x=$\sqrt{2{x}^{2}-48x+290}$,
解得:x=5,或x=-29(舍去).
∴EI=2×5=10.
故八边形的边长为10.
点评 本题考查了翻折变换中的折叠问题、勾股定理以及解无理方程,解题的关键是:(1)根据边与边之间的关系计算出线段NI、NE的长;(2)列出关于x的无理方程.本题属于基础题,难度不大,解决该题型题目时,巧妙的利用勾股定理列出关于x的方程是关键.

练习册系列答案
相关题目
20.经过以下一组点可以画出函数y=2x图象的是( )
| A. | (0,0)和(2,1) | B. | (1,2)和(-1,-2) | C. | (1,2)和(2,1) | D. | (-1,2)和(1,2) |
2.下列计算结果为正数的是( )
| A. | (-$\frac{1}{2}$)3 | B. | (-$\frac{1}{2}$)-2 | C. | -(-$\frac{1}{2}$)0 | D. | -|$\frac{1}{2}$| |
 如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{4}{x}$(x>0)上,则S△OBP=4.
如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{4}{x}$(x>0)上,则S△OBP=4.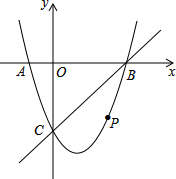 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.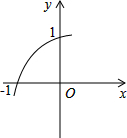 已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2.
已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2. 一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是碳.
一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是碳.