题目内容
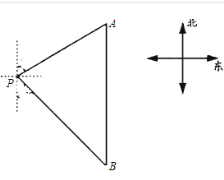
【题目】如图,在平行四边形 ABCD 中,过点 A 作 AE⊥DC 交 DC 的延长线于点 E,过点 D 作DF // EA 交 BA 的延长线于点 F.
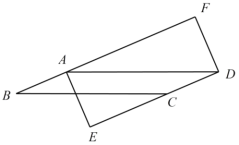
(1)求证:四边形 AEDF 是矩形;
(2)连接BD,若 AB=AE=2,tan FAD ![]() ,求 BD 的长.
,求 BD 的长.
【答案】(1)见解析,(2)![]() .
.
【解析】
(1)由四边形ABCD是平行四边形,AE⊥DC,DF⊥BA,易证得四边形AEDF是平行四边形,继而证得四边形AEDF是矩形;
(2)由四边形AEDF是矩形,可得在Rt△AFD中tan∠FAD=![]() =
=![]() ,继而求得BF的长,然后由勾股定理求得答案.
,继而求得BF的长,然后由勾股定理求得答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,即AF∥ED,
∵AE⊥DC,DF⊥BA,
∴DF∥EA, ∴四边形AEDF是平行四边形,
∵AE⊥DE, ∴∠E=90°,
∴四边形AEDF是矩形;
(2)如图,连接BD, ∵四边形AEDF是矩形,AB=AE=2
∴FD=AE=2,∠F=90°,
∵在Rt△AFD中,tan∠FAD=![]() =
=![]() ,
,
![]() AF=5,
AF=5,
![]() AB=2, ∴BF=AB+AF=7,
AB=2, ∴BF=AB+AF=7,
在Rt△BFD中,BD=![]() .
.


练习册系列答案
相关题目
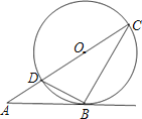
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在 点
在 点![]() 左侧),对称轴为直线
左侧),对称轴为直线![]() .
.
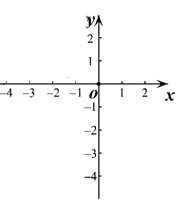
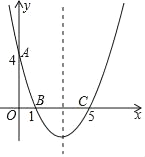
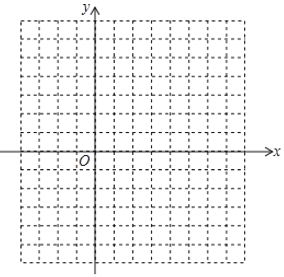
(1)![]() 的值为 ,在坐标系中利用描点法画出此抛物线;
的值为 ,在坐标系中利用描点法画出此抛物线;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直线![]() 过点
过点![]() 且与抛物线交于点
且与抛物线交于点![]() ,请根据图象写出:当
,请根据图象写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .