Question

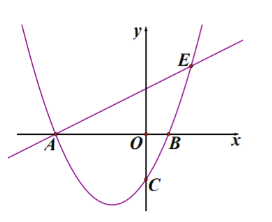
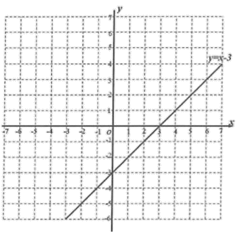
【题目】如图，在平面直角坐标系中，直线交轴于点，交轴于点，点是射线上一动点（点不与点，重合），过点作垂直于轴，交直线于点，以直线为对称轴，将翻折，点的对称点落在轴上，以，为邻边作平行四边形．设点，与重叠部分的面积为．

（1）的长是__________，的长是___________（用含的式子表示）；

（2）求关于的函数关系式，并写出自变量的取值范围．

Answer 1

【答案】（1），；（2）

【解析】

（1）将y=0代入一次函数解析式中即可求出点A的坐标，从而求出结论；

（2）先求出点B的坐标，然后根据锐角三角函数求出，，然后根据m的取值范围分类讨论，分别画出对应的图形，利用相似三角形的判定及性质和各个图形的面积公式计算即可．

解：（1）将y=0代入中，得

解得：x=4

∴点A的坐标为（4,0）

∴OA=4，AP=

故答案为：；．

（2）令，，即

∵垂直于轴，

∴

∴

∵

当时，

∴

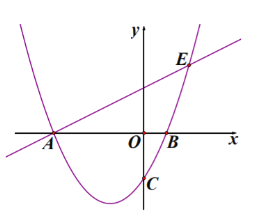
当时，如图2，过点作于点，

由题意知，

∴四边形是平行四边形，

∴

∴，

∴

∴，，

∵，

∴

∴

∵，

∴

∴

当时，如图3，由②知，xE=2

综上