题目内容
已知关于x的一元二次方程x2-(k+2)x+2k=0(k为常数).
(1)求证:无论k取何实数,该方程总有实数根;
(2)若该方程的两根互为倒数,求该方程的两根.
(1)求证:无论k取何实数,该方程总有实数根;
(2)若该方程的两根互为倒数,求该方程的两根.
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)先计算判别式的值得到△=(k-2)2,然后根据非负数的性质得△≥0,则根据判别式的意义得到结论;
(2)根据根与系数的关系得到2k=1,解得k=
,原方程变形为x2-
x+1=0,整理得2x2-5x+2=0,然后利用因式分解法解方程.
(2)根据根与系数的关系得到2k=1,解得k=
| 1 |
| 2 |
| 5 |
| 2 |
解答:(1)证明:∵△=(k+2)2-4×2k=k2-4k+4=(k-2)2≥0,
∴无论k取何实数,该方程总有实数根;
(2)解:根据题意得2k=1,解得k=
,
原方程变形为x2-
x+1=0,
整理得2x2-5x+2=0,
(2x-1)(x-2)=0,
解得x1=
,x2=2.
∴无论k取何实数,该方程总有实数根;
(2)解:根据题意得2k=1,解得k=
| 1 |
| 2 |
原方程变形为x2-
| 5 |
| 2 |
整理得2x2-5x+2=0,
(2x-1)(x-2)=0,
解得x1=
| 1 |
| 2 |
点评:本题考查了一元二次方程根的判别式(△=b2-4ac):一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
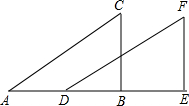 已知:如图,AC=DF,BC=EF,下列条件中,不能证明△ABC≌DEF的是( )
已知:如图,AC=DF,BC=EF,下列条件中,不能证明△ABC≌DEF的是( )| A、AC∥DF |
| B、AD=BE |
| C、∠CBA=∠FED=90° |
| D、∠C=∠F |
 实数a,b在数轴上对应点的位置如图所示,则ab
实数a,b在数轴上对应点的位置如图所示,则ab