题目内容
将下列各式因式分解:
(1)x3-x
(2)-3ma2+12ma-12m
(3)n2(m-2)+4(2-m)
(4)(x+y)2+2(x+y+1)-1.
(1)x3-x
(2)-3ma2+12ma-12m
(3)n2(m-2)+4(2-m)
(4)(x+y)2+2(x+y+1)-1.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)根据提取公因式,可得平方差公式,再根据平方差公式,可得答案;
(2)根据提取公因式,可得完全平方公式,再根据完全平方公式,可得答案;
(3)根据提取公因式,可得平方差公式,再根据平方差公式,可得答案;
(4)根据完全平方公式,可得答案.
(2)根据提取公因式,可得完全平方公式,再根据完全平方公式,可得答案;
(3)根据提取公因式,可得平方差公式,再根据平方差公式,可得答案;
(4)根据完全平方公式,可得答案.
解答:解:(1)原式=x(x2-1)
=x(x+1)(x-1);
(2)原式=-3m(a2-4a+4)
=-3m(a-2)2;
(3)原式=(m-2)(n2-4)
=(m-2)(n+2)(n-2);
(4)原式=(x+y)2+2(x+y)+1
=[(x+y)+1]2
=(x+y+1)2.
=x(x+1)(x-1);
(2)原式=-3m(a2-4a+4)
=-3m(a-2)2;
(3)原式=(m-2)(n2-4)
=(m-2)(n+2)(n-2);
(4)原式=(x+y)2+2(x+y)+1
=[(x+y)+1]2
=(x+y+1)2.
点评:本题考查了因式分解,利用了提取公因式法,再套用公式,注意分解要彻底.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
神龙汽车公司某车间a人b天可生产c个零件,那么a2个人c2天可生产零件数为( )
A、
| ||
B、
| ||
C、
| ||
| D、a2c2 |

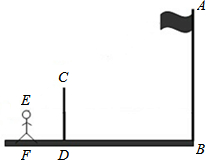 如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.
如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.