题目内容
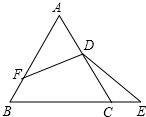 如图,等边△ABC中,D为AC中点,∠EDF=120°,当点F在线段AB上,点E在BC的延长线上.
如图,等边△ABC中,D为AC中点,∠EDF=120°,当点F在线段AB上,点E在BC的延长线上.(1)AF、CE与AB之间的数量关系是
(2)BE、BF与AB之间的数量关系是
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质得出AB=AC=BC,∠A=∠B=∠ACB=60°,求出DG=DC,∠GDF=∠CDE,根据ASA推出△DCE≌△DGF,根据全等三角形的性质得出CE=GF,即可得出答案;
(2)根据上题证得的全等可以得到GF=BE,进而可以得出结论;
(2)根据上题证得的全等可以得到GF=BE,进而可以得出结论;
解答:
证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠A=∠B=∠ACB=60°,
∵D为AC的中点,
∴AD=DC=
AC,
∵DG∥BC,
∴∠AGD=∠B=∠ADG=∠C=60°,
∴△ADG为等边三角形.
∴AG=DG=AD,
∴DG=DC,
∵∠EDF=∠GDC=120°,
∴∠GDF=∠CDE,
在△DCE和△DGF中,
,
∴△DCE≌△DGF(SAS);
∴CE=GF,
∴AF-CE=AF-GF=AG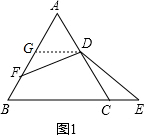 =
=
AB,
即:AF-CE=
AB,
故答案为:AF-CE=
AB.
(2)∵△GDFF≌△CDE,
∴DF=DE.DG=DC.
∵BE+BF=BC+GF+BF,
∴BE+BF=BG+BC
设BA=BC=AC=2a,
∴CD=AD=BG=a,
∴BC+BG=3a,
∴BC+BG=
AB,
即:BE+BF=
AB.
故答案为:BE+BF=
AB.
∴AB=AC=BC,∠A=∠B=∠ACB=60°,
∵D为AC的中点,
∴AD=DC=
| 1 |
| 2 |
∵DG∥BC,
∴∠AGD=∠B=∠ADG=∠C=60°,
∴△ADG为等边三角形.
∴AG=DG=AD,
∴DG=DC,
∵∠EDF=∠GDC=120°,
∴∠GDF=∠CDE,
在△DCE和△DGF中,
|
∴△DCE≌△DGF(SAS);
∴CE=GF,
∴AF-CE=AF-GF=AG
 =
=| 1 |
| 2 |
即:AF-CE=
| 1 |
| 2 |
故答案为:AF-CE=
| 1 |
| 2 |
(2)∵△GDFF≌△CDE,
∴DF=DE.DG=DC.
∵BE+BF=BC+GF+BF,
∴BE+BF=BG+BC
设BA=BC=AC=2a,
∴CD=AD=BG=a,
∴BC+BG=3a,
∴BC+BG=
| 3 |
| 2 |
即:BE+BF=
| 3 |
| 2 |
故答案为:BE+BF=
| 3 |
| 2 |
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,线段中点的性质的运用,解答时正确作辅助线证明三角形全等是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD等于( )cm.
如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD等于( )cm.| A、2 | B、3 | C、4 | D、5 |
某住宅小区6月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31.那么,请你估计该小区6月份(30天)的总用水量的吨数约是( )
| A、960 | B、192 |
| C、5760 | D、32 |
已知样本数据1,4,2,3,4,5,这组数据的中位数是( )
| A、3 | B、4 | C、3.5 | D、2.5 |
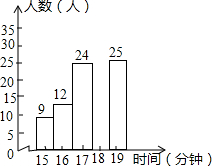 为解决“一票难求”的烦恼,2012年1月1日起,火车票实名制在全国范围内开始实施,某火车站为了改进服务,随机抽查了100名旅客从开始在购票窗口排队到购车票所用的时间t(简称为购票时间,单位:分钟),如图是这次调查数据整理后得到的统计图,请你根据图中的信息,回答下列问题:
为解决“一票难求”的烦恼,2012年1月1日起,火车票实名制在全国范围内开始实施,某火车站为了改进服务,随机抽查了100名旅客从开始在购票窗口排队到购车票所用的时间t(简称为购票时间,单位:分钟),如图是这次调查数据整理后得到的统计图,请你根据图中的信息,回答下列问题: 如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.
如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.