题目内容
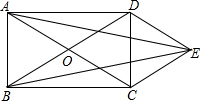 如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
考点:矩形的性质,全等三角形的判定与性质,菱形的判定
专题:几何图形问题
分析:(1)首先利用平行四边形的判定得出四边形DOCE是平行四边形,进而利用矩形的性质得出DO=CO,即可得出答案;
(2)利用等腰三角形的性质以及矩形的性质得出AD=BC,∠ADE=∠BCE,进而利用全等三角形的判定得出.
(2)利用等腰三角形的性质以及矩形的性质得出AD=BC,∠ADE=∠BCE,进而利用全等三角形的判定得出.
解答:(1)证明:∵DE∥AC,CE∥BD,
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC、BD相交于点O,
∴OC=
AC=
BD=OD,
∴四边形OCED为菱形;
(2)解:AE=BE.
理由:∵四边形OCED为菱形,
∴ED=CE,∴∠EDC=∠ECD,
∴∠ADE=∠BCE,
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴AE=BE.
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC、BD相交于点O,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形OCED为菱形;

(2)解:AE=BE.
理由:∵四边形OCED为菱形,
∴ED=CE,∴∠EDC=∠ECD,
∴∠ADE=∠BCE,
在△ADE和△BCE中,
|
∴△ADE≌△BCE(SAS),
∴AE=BE.
点评:此题主要考查了矩形的性质以及菱形的判定和全等三角形的判定与性质等知识,熟练掌握矩形的性质进而得出对应线段关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在?ABCD中,∠BAD的平分线AE交BC的延长线于点E,AB=10,BC=6,则CE的长为( )
如图,在?ABCD中,∠BAD的平分线AE交BC的延长线于点E,AB=10,BC=6,则CE的长为( )| A、1 | B、2 | C、3 | D、4 |
下列说法正确的是( )
| A、一元二次方程的一般形式是ax2+bx+c=0 | ||||
| B、方程x2=x的解是x=1 | ||||
C、一元二次方程的一般形式是ax2+bx+c=0 的根是x=
| ||||
| D、方程x(x+2)(x-3)=0的实数根有三个 |
 已知Rt△ABO中,AB=OB=2,∠ABO=90°.以AB为边,在Rt△ABO的右边作等边△ABC,如图所示,求点O与点C的距离.
已知Rt△ABO中,AB=OB=2,∠ABO=90°.以AB为边,在Rt△ABO的右边作等边△ABC,如图所示,求点O与点C的距离.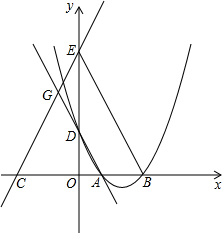 已知抛物线y=x2-(k+2)x+
已知抛物线y=x2-(k+2)x+ 在△ABC中,过三角形的三个顶点A、B、C向它的对边作垂线,垂足分别为D、E、F,若AC=5cm,BE=6cm,求△ABC的面积.
在△ABC中,过三角形的三个顶点A、B、C向它的对边作垂线,垂足分别为D、E、F,若AC=5cm,BE=6cm,求△ABC的面积. 图中表示的不等式的解集是
图中表示的不等式的解集是