题目内容
如图，正方形ABCD边长为2，对角线AC、BD相交于点O，E是AB中点，则OE的长为考点：正方形的性质
专题：
分析：证明AO=CO；由AE=BE得到OE为△ABC的中位线，即可解决问题．
解答：解：∵四边形ABCD为正方形，
∴AO=CO；而AE=BE，
∴OE是△ABC的中位线，
∴OE=
×2=1．
解：∵四边形ABCD为正方形，∴AO=CO；而AE=BE，
∴OE是△ABC的中位线，
∴OE=
| 1 |
| 2 |
点评：该题主要考查了正方形的性质、三角形的中位线定理及其应用问题；牢固掌握正方形的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后，1.5小时内其血液中含药量y（微克/毫升）与时间x（时）的关系可近似地用二次函数y=-12x2+24x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数将数轴上表示-5的点，先向右移动两个单位长度，再向左移动三个单位长度后对应的点表示的数是（ ）
| A、-1 | B、-4 | C、4 | D、-6 |
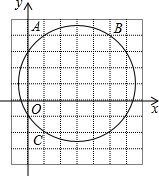如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，4），（5，4），（1，-2），则以A，B，C为顶点的三角形外接圆的圆心坐标是（ ）| A、（2，3） |
| B、（3，2） |
| C、（3，1） |
| D、（1，3） |