题目内容
(10分)如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求cosA的值.
(1)详见解析;(2) .
.
【解析】
试题分析:(1)证得OD⊥DE,根据切线的判定定理得到DE是⊙O的切线;
(2)由OD//AE,得到 ,通过转换得到
,通过转换得到 ,解得FC的长,进而求得AF的长,应用锐角三角函数求出cosA的值.
,解得FC的长,进而求得AF的长,应用锐角三角函数求出cosA的值.
试题解析:【解析】
(1)证明:连结AD、OD,
∵AC是直径,
∴AD⊥BC,
∵AB=AC,
∴D是BC的中点,
又∵O是AC的中点
∴OD//AB,
∵DE⊥AB,
∴OD⊥DE,
∴DE是⊙O的切线;

(2)由(1)知OD//AE,
∴ ,
,
∴ ,
,
∴ ,
,
解得FC=2,
∴AF=6,
∴cosA= .
.
考点:1、切线的判定;2、平行线分线段成比例定理;3、锐角三角函数.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目

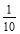 ,-3.5,-0.01,-2,-212各数中,最大的数是 .
,-3.5,-0.01,-2,-212各数中,最大的数是 . B.1.1?
B.1.1? C.1.1?
C.1.1? D.0.11?
D.0.11?
 ,则平移的距离是 .
,则平移的距离是 .

 B.
B. C.
C. D.
D.