题目内容
9.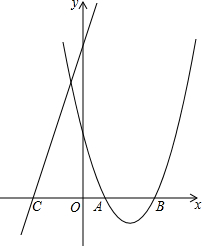 已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2
已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2(1)求证:无论k取何实数值,抛物线与x轴有两个不同的交点;
(2)抛物线与x轴交于点A,B,直线与x轴交于点C,设A,B,C三点的横坐标分别是x1,x2,x3,求x1•x2•x3的最大值.
分析 (1)令y=0得到关于x的一元二次方程,然后根据一元二次方程根的判别式进行判定即可;
(2)由韦达定理可求得${x}_{1}•{x}_{2}=\frac{5k+2}{4}$,y=0可求得:x3=-(k+1),然后列出x1•x2•x3与k的函数关系式,最后利用配方法即可求得其最大值.
解答 解:(1)△=${b}^{2}-4ac=[-(k+2)]^{2}-4×1×\frac{5k+2}{4}$
=k2+4k+4-5k-2
=k2-k+2
=$(k-\frac{1}{2})^{2}+\frac{7}{4}$
∴△>0.
∴抛物线与x轴有两个不同的交点.
(2)由韦达定理可知:${x}_{1}•{x}_{2}=\frac{5k+2}{4}$,
令直线方程y=0得:(k+1)x+(k+1)2=0,解得:x3=-(k+1),
∴x1•x2•x3=-(k+1)×$\frac{5k+2}{4}$=$-\frac{5}{4}(k+\frac{7}{10})^{2}+\frac{9}{80}$.
当k=$-\frac{7}{10}$时,x1•x2•x3有最大值,最大值为$\frac{9}{80}$.
点评 本题主要考查的是二次函数的最值和一元二次方程根的判别式、根与系数关系的应用,将函数问题转化为方程问题是解题解题的关键.

练习册系列答案
相关题目
1.化简$\sqrt{{{(-8)}^2}}$的结果是( )
| A. | -8 | B. | 8 | C. | ±4 | D. | ±8 |
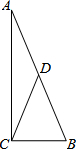 如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7.
如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7. 如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点.
如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点.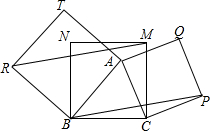 如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.
如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.