题目内容
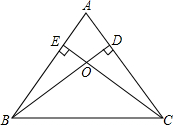 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.
如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.考点:等腰三角形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:根据等边对等角可得∠ABC=∠ACB,然后利用“角角边”证明△BCE和△CBD全等,根据全等三角形对应角相等可得∠BCE=∠CBD,再利用等角对等边即可得证.
解答:证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD⊥AC,CE⊥AB,
∴∠BDC=∠CEB=90°,
在△BCE和△CBD中,
,
∴△BCE≌△CBD(AAS),
∴∠BCE=∠CBD,
∴BO=CO.
∴∠ABC=∠ACB,
∵BD⊥AC,CE⊥AB,
∴∠BDC=∠CEB=90°,
在△BCE和△CBD中,
|
∴△BCE≌△CBD(AAS),
∴∠BCE=∠CBD,
∴BO=CO.
点评:本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,是基础题,找出△BCE和△CBD全等的条件是解题的关键.

练习册系列答案
相关题目
完成一项工作,甲单做需a天,乙单需做b天,甲、乙、丙合作需c天,则丙单做全部工作所需的天数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,DE是△ABC的中位线,FG为梯形BCED的中位线,若BC=8,则FG等于( )
如图,DE是△ABC的中位线,FG为梯形BCED的中位线,若BC=8,则FG等于( )| A、2 cm |
| B、3 cm |
| C、4 cm |
| D、6 cm |
计算a7•a3的值为( )
| A、a21 |
| B、a4 |
| C、a10 |
| D、2a10 |
反比例函数y=-
与正比例函数y=2x在同一坐标系内的大致图象为( )
| 1 |
| x |
A、 |
B、 |
C、 |
D、 |
 已知;如图,AD∥BC,AD=BC,
已知;如图,AD∥BC,AD=BC,


