题目内容
完成一项工作,甲单做需a天,乙单需做b天,甲、乙、丙合作需c天,则丙单做全部工作所需的天数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列代数式(分式)
专题:
分析:根据甲单做需a天,乙单需做b天,甲、乙、丙合作需c天,即可得出每个人单独做一天,完成的总工作量,进而求出丙单做全部工作所需的天数.
解答:解:∵甲单做需a天,乙单需做b天,甲、乙、丙合作需c天,
∴甲每天完成总工作量的:
,乙每天完成总工作量的:
,甲、乙、丙合作每天完成总工作量的:
,
∴丙单做全部工作所需的天数是:
=
.
故选:A.
∴甲每天完成总工作量的:
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴丙单做全部工作所需的天数是:
| 1 | ||||||
|
| abc |
| ab-ac-bc |
故选:A.
点评:此题主要考查了列分式,根据已知得出三人每天完成的总工作量是解题关键.

练习册系列答案
相关题目
 已知有理数a、b、c在数轴上的对应点,分别为A、B、C(如图)
已知有理数a、b、c在数轴上的对应点,分别为A、B、C(如图) 如图,在正方形ABCD中,点P是AB的中点,BE⊥DP的延长线于点E,连接AE,过点A作FA⊥AE交DP于点F,连接BF、FC.下列结论中:①△ABE≌△ADF;②PF=EP+EB;③△BCF是等边三角形;④∠ADF=∠DCF;⑤S△APF=S△CDF.其中正确的是( )
如图,在正方形ABCD中,点P是AB的中点,BE⊥DP的延长线于点E,连接AE,过点A作FA⊥AE交DP于点F,连接BF、FC.下列结论中:①△ABE≌△ADF;②PF=EP+EB;③△BCF是等边三角形;④∠ADF=∠DCF;⑤S△APF=S△CDF.其中正确的是( )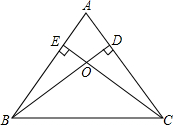 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.
如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.