题目内容
19.计算:($\sqrt{13}$$-\sqrt{14}$)212•($\sqrt{13}+\sqrt{14}$)213的值为$\sqrt{13}$+$\sqrt{14}$.分析 先根据积的乘方得到原式=[($\sqrt{13}$$-\sqrt{14}$)•($\sqrt{13}+\sqrt{14}$)]212•($\sqrt{13}$+$\sqrt{14}$),然后利用平方差公式计算即可.
解答 解:原式=[($\sqrt{13}$$-\sqrt{14}$)•($\sqrt{13}+\sqrt{14}$)]212•($\sqrt{13}$+$\sqrt{14}$)
=(13-14)212•($\sqrt{13}$+$\sqrt{14}$)
=$\sqrt{13}$+$\sqrt{14}$..
故答案为$\sqrt{13}$+$\sqrt{14}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列说法错误的是( )
| A. | 一个非零数与其倒数之积为1 | |
| B. | 一个数与其相反数之商为-1 | |
| C. | 若两个数的商为-1,则这两个数互为相反数 | |
| D. | 若两个数的积为1,则这两个数互为倒数 |
 如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为14.
如图,△AOB≌△DOC,△AOB的周长为10,且BC=4,则△DBC的周长为14.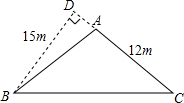 如图所示,有一块三角形ABC空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价300元,AC=12m,BD=15m.
如图所示,有一块三角形ABC空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价300元,AC=12m,BD=15m. 如图是一个长与宽之比为2:1的长方形草坪,其对角线长为$\sqrt{125}$米,现欲改造成一个面积相等的正方形草坪,则改造后的正方形草坪的边长为5$\sqrt{2}$米.
如图是一个长与宽之比为2:1的长方形草坪,其对角线长为$\sqrt{125}$米,现欲改造成一个面积相等的正方形草坪,则改造后的正方形草坪的边长为5$\sqrt{2}$米.