题目内容
12.抛物线y=x2+bx+c与y轴交于C,与x轴交于A,B,且OB>OA.(1)判断b的符号;
(2)若AB为直径的圆恰好过C点交y轴于D,求D坐标.
分析 (1)根据OB>OA,判断对称轴的位置,可以判断b的符号;
(2)根据对称性可知,点D与点C关于x轴对称,得到点D的坐标.
解答 解:(1)∵OB>OA,
∴对称轴在y轴的右侧,
即-$\frac{b}{2}$>0,
∴b<0;
(2)∵点C的坐标为:(0,c),
由题意得,点D与点C关于x轴对称,
∴点D的坐标为:(0,-c).
点评 本题考查的是二次函数图象与系数的关系,根据开口方向和对称轴的位置可以确定a、b的符号,即左同右异.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.-2015的相反数是( )
| A. | 2015 | B. | $\frac{1}{2015}$ | C. | -$\frac{1}{2015}$ | D. | -2015 |
7.测定某运动员跑100m的平均速度,测的结果是跑完前24m用了3s,跑完后76m又用了6s,该运动员的平均速度是( )
| A. | 8m/s | B. | 11.1m/s | C. | 12.7m/s | D. | 10.35m/s |

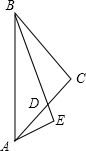 如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,
如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,