题目内容
19．
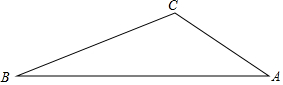如图，在△ABC中，∠B=30°，AC=2$\sqrt{3}$，BC=6，求sinA的值．
分析 作高线CD，构建两个直角三角形，先根据30°角所对的直角边是斜边的一半求CD的长，所以在Rt△ACD中，利用三角函数的定义可得结论．
解答 
解：过C作CD⊥AB，垂足为D，
在Rt△BCD中，∵∠B=30°，BC=6，
∴CD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3，
在Rt△ACD中，∵AC=2$\sqrt{3}$，
∴sin∠A=$\frac{CD}{AC}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$．
点评 本题是解直角三角形，熟练掌握三角函数的定义是关键，同时还运用了直角三角形中30°角的性质，本题属于基础题．
练习册系列答案
相关题目
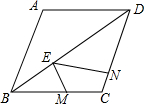已知，如图，菱形ABCD中，∠ABC=60°，E为线段DB上的一点，∠MEN=60°，点M，N分别在直线BC，DC上．
如图，已知点A、B是数轴上的两点，O为原点，点B对应的数为3，AB=10．