题目内容
关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都没有实数根 |
| B、k为任何实数,方程都有两个不相等的实数根 |
| C、k为任何实数,方程都有两个相等的实数根 |
| D、k取值不同实数,方程实数根的情况有三种可能 |
考点:根的判别式
专题:
分析:先计算判别式的值得到△=4k2+4,根据非负数的性质得△>0,然后根据判别式的意义进行判断.
解答:解:△=4k2-4×(-1)
=4k2+4,
∵4k2≥0,
∴4k2+4>0
∴方程有两个不相等的实数根.
故选B.
=4k2+4,
∵4k2≥0,
∴4k2+4>0
∴方程有两个不相等的实数根.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
等腰三角形的周长是31,其中一边长为7cm,等腰三角形的底边长是( )
| A、12cm | B、7cm |
| C、17cm | D、7cm或17cm |
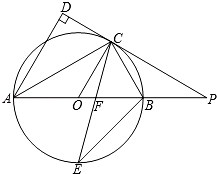 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.