题目内容
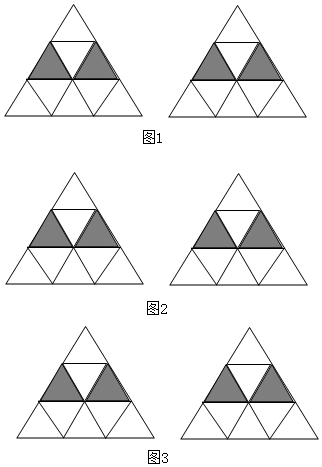
5.在一节数学活动课上,李老师给出如下图形,正三角形网格中,已有两个小正三角形被涂黑,按要求分析后解答:(1)再将图1中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,则有3种不同的画法.(画出其中两种,左右两图各画一种);
(2)再将图2中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形,则有5种不同的画法.(画出其中两种,左右两图各画一种).
(3)再将图3中其余小三角形涂黑三个,使整个被涂黑的图案构成一个轴对称图形,则有7种不同的画法.(画出其中两种,左右两图各画一种).
分析 根据轴对称图形的性质,一一画出符合题意的图形即可.
解答 解:(1)再将图1中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形,则有3种不同的画法.如图1中所示.
(2)再将图2中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形,则有5种不同的画法,如图2中所示.
(3)再将图3中其余小三角形涂黑三个,使整个被涂黑的图案构成一个轴对称图形,则有7种不同的画法.如图3中所示.
点评 本题考查轴对称图形的性质、等边三角形的性质等知识,解题的关键是认真观察图形,寻找规律解决问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
15.下列计算正确的是( )
| A. | $\frac{{\sqrt{27}}}{3}=9$ | B. | $(\sqrt{2}+\sqrt{5}{)^2}=7$ | C. | $\sqrt{(\sqrt{3}-2{)^2}}=\sqrt{3}-2$ | D. | $\sqrt{12}-\sqrt{3}=\sqrt{3}$ |
16.已知∠A=37°17',则∠A的余角等于( )
| A. | 37°17' | B. | 52°83' | C. | 52°43' | D. | 142°43' |
17.下列运算正确的是( )
| A. | a3+a2=a5 | B. | (a3)2=a5 | C. | (a+b)2=a2+b2 | D. | a2•a4=a6 |
17.若a,b,c为直角三角形的三边长,且a,b满足$\sqrt{{b}^{2}-16}+{a}^{2}+9=6a$,则斜边的长为( )
| A. | 5 | B. | 5或$\sqrt{7}$ | C. | 5或4 | D. | 5或4或3 |
 对若干名青少年进行最喜爱的运动项目的问卷调查,并根据调查结果绘制如图所示的扇形统计图,如果最喜爱足球的人数比最喜爱游泳的人数多40人,则这次参加问卷调查的总人数为200人.
对若干名青少年进行最喜爱的运动项目的问卷调查,并根据调查结果绘制如图所示的扇形统计图,如果最喜爱足球的人数比最喜爱游泳的人数多40人,则这次参加问卷调查的总人数为200人.