题目内容
14.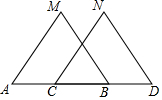 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AM∥CN | C. | AB=CD | D. | AM=CN |
分析 根据三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证即可.
解答 解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;
B、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.
C、AB=CD,符合SAS,能判定△ABM≌△CDN,故B选项不符合题意;
D、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故C选项符合题意;
故选D.
点评 本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,本题是一道较为简单的题目.

练习册系列答案
相关题目
5.已知二次函数y=ax2+bx+1(a≠0)的图象过点(1,0),且顶点在第二象限,设P=a-b,则P的取值范围是( )
| A. | -1<P<0 | B. | -1<P<1 | C. | 0<P<1 | D. | 1<P<2 |
2.$-\frac{1}{8}$的倒数是( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | -8 | D. | -1 |
9.在有理数中,有( )
| A. | 最小的数 | B. | 最大的数 | C. | 绝对值最小的数 | D. | 绝对值最大的数 |
19. 如图,五边形ABCDE中,AB∥CD,则图中x的值是( )
如图,五边形ABCDE中,AB∥CD,则图中x的值是( )
 如图,五边形ABCDE中,AB∥CD,则图中x的值是( )
如图,五边形ABCDE中,AB∥CD,则图中x的值是( )| A. | 75° | B. | 65° | C. | 60° | D. | 55° |
6.下列各式计算正确的是( )
| A. | -32=-6 | B. | (-3)2=-9 | C. | -32=-9 | D. | -(-3)2=9 |
3.若正比例函数的图象经过点(-1,2),(-m,4-2m),则m的值为( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
4.下列运算能用平方差公式的是( )
| A. | (a+b)(-a+b) | B. | (m+n)(m+n) | C. | (-2x+y)(2x-y) | D. | -(p-q)(q-p) |
 如图,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE顶点D与边AB的中点重合,DE,DF分别交AC于点P,Q,若重叠部分△DPQ是以DP为一腰的等腰三角形,则它的面积为$\frac{5}{2}$或2$\sqrt{5}$-2.
如图,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE顶点D与边AB的中点重合,DE,DF分别交AC于点P,Q,若重叠部分△DPQ是以DP为一腰的等腰三角形,则它的面积为$\frac{5}{2}$或2$\sqrt{5}$-2.