题目内容
7.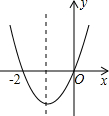 如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:
如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:①a+b+c>0;
②该抛物线的对称轴是直线x=-1;
③当x=1时,y=2a;
④am2+bm+a>0(m≠-1).
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①利用x=1时y>0进行分析判断;
②由抛物线经过(-2,0),(0,0)可以判断出对称轴为直线x=-1;
③由x=1时,y=a+b+c,再结合抛物线的对称轴为x=-1可得b=2a,抛物线经过原点得到c=0,据此进行推理分析;
④由当x=m时,对应的函数值为y=am2+bm+c,当x=-1时,对应的函数值为y=a-b+c,并结合当x=-1时函数有最小值进行分析判断.
解答 解:根据抛物线可知:当x=1时y>0,则有a+b+c>0,故①正确;
由二次函数的图象可知,抛物线经过点(-2,0),(0,0),开口向上,
∴抛物线的对称轴为直线x=-1,故②正确;
当x=1时,y=a+b+c,
∵抛物线的对称轴是直线x=-1,
∴$-\frac{b}{2a}$=-1,
∴b=2a,
又∵抛物线经过(0,0),
∴c=0,
∴y=3a,故③错误;
当x=m时,对应的函数值为y=am2+bm+c,
当x=-1时,对应的函数值为y=a-b+c,
又∵x=-1时函数取得最小值,
∴a-b+c<am2+bm+c,即a-b<am2+bm,
∵b=2a,
∴am2+bm+a>0(m≠-1),故④正确;
故选C.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定,解答此类问题要注意数形结合思想的运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.改革开放以来,我国国内生产总值由1978年的3645亿元增长到2014年的约63.6万亿元.将近似数63.6万亿元用科学记数法表示应为( )
| A. | 6.36×1012 | B. | 63.6×1012 | C. | 6.36×1013 | D. | 6.36×1014 |
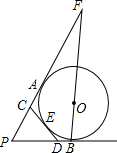 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.延长BO交PA的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r.
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.延长BO交PA的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r.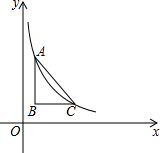 如图,在平面直角坐标系中,Rt△ABC的边AB垂直于x轴,BC=4,点A的纵坐标为9,反比例函数y=$\frac{18}{x}$(x>0)的图象经过点A、C.
如图,在平面直角坐标系中,Rt△ABC的边AB垂直于x轴,BC=4,点A的纵坐标为9,反比例函数y=$\frac{18}{x}$(x>0)的图象经过点A、C. 如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.
如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.