题目内容
12.计算:(1)解方程:(x+1)(x-1)+2(x+3)=8;
(2)化简下式,再求值:(-x2+3-7x)+(5x-7+2x2),其中x=$\sqrt{2}$+1.
分析 (1)方程整理后,利用因式分解法求出解即可;
(2)原式去括号合并得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原方程可化为 x2+2x-3=0,
整理得:(x+3)(x-1)=0,
解得:x1=-3,x2=1;
(2)原式=-x2+3-7x+5x-7+2x2=x2-2x-4=(x-1)2-5,
把x=$\sqrt{2}$+1代入得:原式=($\sqrt{2}$+1-1)2-5=2-5=-3.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
7.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是( )


| A. | 轴对称变换 | B. | 平移变换 | C. | 旋转变换 | D. | 中心对称变换 |
4.昌平区兴寿镇草莓种植户张强、李亮,均在自家的大棚里种植了丰香和章姬两个品种的草莓,两个种植户的草莓种植面积与纯收入如表:
(说明:同类草莓每亩平均纯收入相等)
(1)求丰香和章姬两类草莓每亩平均纯收入各是多少万元?
(2)王刚准备租20亩地用来种植丰香和章姬两类草莓,为了使纯收入超过10万元,且种植章姬的面积不超过种植丰香的面积的2倍(两类草莓的种植面积均为整数),求种植户王刚所有的种植方案.
| 种植户 | 种植丰香的面积 (单位:亩) | 种植章姬的面积 (单位:亩) | 纯收入 (单位:万元) |
| 张强 | 3 | 1 | 1.8 |
| 李亮 | 2 | 3 | 2.6 |
(1)求丰香和章姬两类草莓每亩平均纯收入各是多少万元?
(2)王刚准备租20亩地用来种植丰香和章姬两类草莓,为了使纯收入超过10万元,且种植章姬的面积不超过种植丰香的面积的2倍(两类草莓的种植面积均为整数),求种植户王刚所有的种植方案.
1. 如图,在平面直角坐标系中,A、B是双曲线y=$\frac{k}{x}$的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是( )
如图,在平面直角坐标系中,A、B是双曲线y=$\frac{k}{x}$的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是( )
 如图,在平面直角坐标系中,A、B是双曲线y=$\frac{k}{x}$的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是( )
如图,在平面直角坐标系中,A、B是双曲线y=$\frac{k}{x}$的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是( )| A. | 0<b<1 | B. | 0<b<2 | C. | b>1 | D. | b<2 |
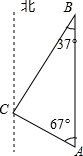 如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离.
如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=$\frac{5}{2}$或$\frac{11}{3}$或$\frac{31}{3}$,△APE的面积等于10.
如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=$\frac{5}{2}$或$\frac{11}{3}$或$\frac{31}{3}$,△APE的面积等于10. 如图,已知OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.
如图,已知OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.