题目内容
一块长36m．宽24m的矩形草地，现要在它的中央修建一个矩形喷水池，周围的草地为走道，走道的宽度相等，且喷水池的面积是原矩形草地面积的
，求周围走道的宽度．
| 5 |
| 27 |
考点：一元二次方程的应用
专题：几何图形问题
分析：根据题意表示出矩形喷水池的面积，进而得出等式求出即可．
解答：解：设周围走道的宽度为xm，根据题意可得：
（36-2x）（24-2x）=36×24×
，
整理得：x2-30x+176=0，
解得：x1=8，x2=22（不合题意舍去）．
答：周围走道的宽度为8m．
（36-2x）（24-2x）=36×24×
| 5 |
| 27 |
整理得：x2-30x+176=0，
解得：x1=8，x2=22（不合题意舍去）．
答：周围走道的宽度为8m．
点评：此题主要考查了一元二次方程的应用，根据题意得出正确等量关系是解题关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
在2、-2.5、0、-2这四个数中，最小的是（ ）
| A、2 | B、-2.5 | C、0 | D、-2 |
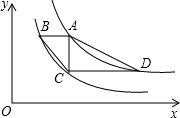如图，点A是函数y=