Question

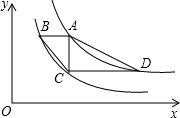如图，点A是函数y=

2

x

（x＞0）图象上任意一点，过点A分别作x，y轴平行线交函数y=

1

x

（x＞0）图象于点B、C，过C点作x轴的平行线交函数y=

2

x

图象于点D．
（1）设A点横坐标为a，试用a表示B、C点坐标．
（2）求四边形ABCD的面积．

Answer 1

考点：反比例函数图象上点的坐标特征,反比例函数系数k的几何意义

专题：

分析：（1）设A点的横坐标为a，由AC∥y轴，AB∥x轴，则C点坐标为（a，

1

a

），B点的纵坐标为

2

a

，把y=

2

a

代入y=

1

x

即可求得B点坐标为（

a

2

，

2

a

）；
（2）由CD∥x轴，求得D的坐标，即可求得AB、AC、CD的长，然后根据S_{四边形ABCD}=S_△ABC+S_△ACD即可求得四边形ABCD的面积．

解答：解：（1）设A点的横坐标为a，把x=a代入y=

2

x

得y=

2

a

，则点A的坐标为（a，

2

a

），
∵AC∥y轴，AB∥x轴，
∴C点坐标为（a，

1

a

），B点的纵坐标为

2

a

；
∴

2

a

=

1

x

，
解得x=

a

2

．
∴B点坐标为（

a

2

，

2

a

）；

（2）∵C点坐标为（a，

1

a

），CD∥x轴，
∴D点纵坐标为

1

a

，
∴

1

a

=

2

x

，解得x=2a，
∴D的坐标为（2a，

1

a

）
∵AB=a-

a

2

=

a

2

，AC=

2

a

-

1

a

=

1

a

，CD=2a-a=a，
∴S_{四边形ABCD}=S_△ABC+S_△ACD=

1

2

AB•AC+

1

2

AC•CD=

1

2

AC（AB+CD）=

1

2

×

1

a

×（

a

2

+a）=

3

4

．

点评：本题考查了反比例函数综合题：点在反比例函数图象上，点的横纵坐标满足反比例函数图象的解析式；平行于x轴的直线上的所有点的纵坐标相同；平行于y轴的直线上的所有点的横坐标相同；