��Ŀ����
��ͼ1������OABC����B������Ϊ��8��3��������D������Ϊ��12��0��������P�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x��������������˶�������Q�ӵ�D��������ÿ��1����λ���ȵ��ٶ���x��ĸ����������˶���PQ����ͬʱ�˶�������ʱֹͣ�����˶������У���PQΪб����x���Ϸ�������ֱ��������PQR�����˶�ʱ��Ϊt�룮
��1����t= ʱ����PQR�ı�QR������B��
��2�����PQR�;���OABC�ص����ֵ����ΪS����S����t�ĺ�����ϵʽ��
��3����ͼ2��������E��5��0����EF��BC������ΪF������PQR�Ķ���R���ھ���OABC���ڲ�ʱ������R��x�ᡢy���ƽ���ߣ��ֱ�EF��BC�ڵ�M��N������MAN=45�㣬��t��ֵ��
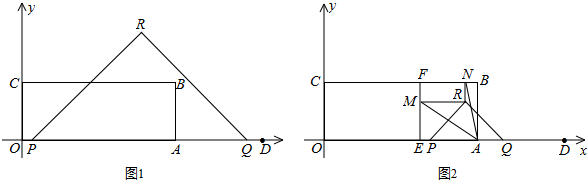
��1����t=
��2�����PQR�;���OABC�ص����ֵ����ΪS����S����t�ĺ�����ϵʽ��
��3����ͼ2��������E��5��0����EF��BC������ΪF������PQR�Ķ���R���ھ���OABC���ڲ�ʱ������R��x�ᡢy���ƽ���ߣ��ֱ�EF��BC�ڵ�M��N������MAN=45�㣬��t��ֵ��
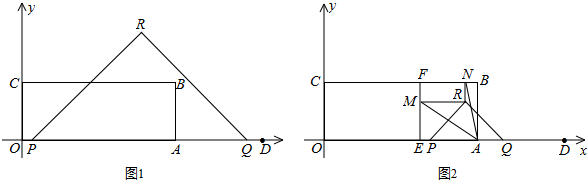
���㣺�ı����ۺ���
ר�⣺�����ۺ���,ѹ����
��������1����PQR�ı�QR������Bʱ����ABQ���ɵ���ֱ�������Σ�����AB=AQ���ɴ��з������t��ֵ��
��2����ͼ���˶��Ĺ����У����������Σ���Ҫ�������ۣ�����©�⣻
��3�������ж�ABFEΪ�����Σ����ͨ����ת����������ȫ��֤��MN=EM+BN����EM=m��BN=n����Rt��FMN�У��ɹ��ɶ����õ���ʽ��mn+3��m+n��-9=0���ɴ˵�ʽ�з������ʱ��t��ֵ��
��2����ͼ���˶��Ĺ����У����������Σ���Ҫ�������ۣ�����©�⣻
��3�������ж�ABFEΪ�����Σ����ͨ����ת����������ȫ��֤��MN=EM+BN����EM=m��BN=n����Rt��FMN�У��ɹ��ɶ����õ���ʽ��mn+3��m+n��-9=0���ɴ˵�ʽ�з������ʱ��t��ֵ��
����⣺��1����PQR�ı�QR������Bʱ����ABQ���ɵ���ֱ�������Σ�
��AB=AQ����3=4-t��
��t=1��
����t=1��ʱ����PQR�ı�QR������B��
��2���ٵ�0��t��1ʱ�����ͼ1-1��ʾ��
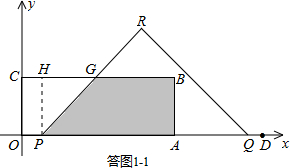
��PR��BC�ڵ�G��
����P��PH��BC�ڵ�H����CH=OP=2t��GH=PH=3��
S=S����OABC-S����OPGC
=8��3-
��2t+2t+3����3
=
-6t��
�ڵ�1��t��2ʱ�����ͼ1-2��ʾ��
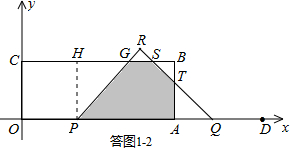
��PR��BC�ڵ�G��RQ��BC��AB�ڵ�S��T��
����P��PH��BC�ڵ�H����CH=OP=2t��GH=PH=3��
QD=t����AQ=AT=4-t��
��BT=BS=AB-AQ=3-��4-t��=t-1��
S=S����OABC-S����OPGC-S��BST
=8��3-
��2t+2t+3����3-
��t-1��2
=-
t2-5t+19��
�۵�2��t��4ʱ�����ͼ1-3��ʾ��
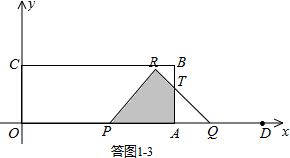
��RQ��AB���ڵ�T����AT=AQ=4-t��
PQ=12-3t����PR=RQ=
��12-3t����
S=S��PQR-S��AQT
=
PR2-
AQ2
=
��12-3t��2-
��4-t��2
=
t2-14t+28��
����������S����t�ĺ�����ϵʽΪ��
S=
��
��3����E��5��0������AE=AB=3��
���ı���ABFE�������Σ�
���ͼ2������AME�Ƶ�A˳ʱ����ת90�㣬�õ���ABM�䣬����AE��AB�غϣ�
�ߡ�MAN=45�㣬
���EAM+��NAB=45�㣬
���BAM��+��NAB=45�㣬
���MAN=��M��AN��
����MN���ڡ�MAN���M��AN�У�
���MAN�ա�M��AN��SAS����
��MN=M��N=M��B+BN
��MN=EM+BN��
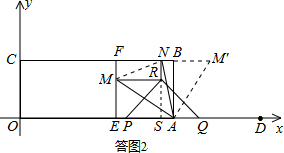
��EM=m��BN=n����FM=3-m��FN=3-n��
��Rt��FMN�У��ɹ��ɶ����ã�FM2+FN2=MN2������3-m��2+��3-n��2=��m+n��2��
�����ã�mn+3��m+n��-9=0�� ��
�ӳ�NR��x���ڵ�S����m=EM=RS=
PQ=
��12-3t����
��QS=
PQ=
��12-3t����AQ=4-t��
��n=BN=AS=QS-AQ=
��12-3t��-��4-t��=2-
t��
��m=3n��
�����ʽ������ã�n2+4n-3=0��
���n=-2+
��n=-2-
����ȥ��
��2-
t=-2+
��ã�t=8-2
��
������MAN=45�㣬��t��ֵΪ��8-2
���룮
��AB=AQ����3=4-t��
��t=1��
����t=1��ʱ����PQR�ı�QR������B��
��2���ٵ�0��t��1ʱ�����ͼ1-1��ʾ��

��PR��BC�ڵ�G��
����P��PH��BC�ڵ�H����CH=OP=2t��GH=PH=3��
S=S����OABC-S����OPGC
=8��3-
| 1 |
| 2 |
=
| 39 |
| 2 |
�ڵ�1��t��2ʱ�����ͼ1-2��ʾ��

��PR��BC�ڵ�G��RQ��BC��AB�ڵ�S��T��
����P��PH��BC�ڵ�H����CH=OP=2t��GH=PH=3��
QD=t����AQ=AT=4-t��
��BT=BS=AB-AQ=3-��4-t��=t-1��
S=S����OABC-S����OPGC-S��BST
=8��3-
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
�۵�2��t��4ʱ�����ͼ1-3��ʾ��

��RQ��AB���ڵ�T����AT=AQ=4-t��
PQ=12-3t����PR=RQ=
| ||
| 2 |
S=S��PQR-S��AQT
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
=
| 7 |
| 4 |
����������S����t�ĺ�����ϵʽΪ��
S=
|
��3����E��5��0������AE=AB=3��
���ı���ABFE�������Σ�
���ͼ2������AME�Ƶ�A˳ʱ����ת90�㣬�õ���ABM�䣬����AE��AB�غϣ�
�ߡ�MAN=45�㣬
���EAM+��NAB=45�㣬
���BAM��+��NAB=45�㣬
���MAN=��M��AN��
����MN���ڡ�MAN���M��AN�У�
|
���MAN�ա�M��AN��SAS����
��MN=M��N=M��B+BN
��MN=EM+BN��

��EM=m��BN=n����FM=3-m��FN=3-n��
��Rt��FMN�У��ɹ��ɶ����ã�FM2+FN2=MN2������3-m��2+��3-n��2=��m+n��2��
�����ã�mn+3��m+n��-9=0�� ��
�ӳ�NR��x���ڵ�S����m=EM=RS=
| 1 |
| 2 |
| 1 |
| 2 |
��QS=
| 1 |
| 2 |
| 1 |
| 2 |
��n=BN=AS=QS-AQ=
| 1 |
| 2 |
| 1 |
| 2 |
��m=3n��
�����ʽ������ã�n2+4n-3=0��
���n=-2+
| 7 |
| 7 |
��2-
| 1 |
| 2 |
| 7 |
��ã�t=8-2
| 7 |
������MAN=45�㣬��t��ֵΪ��8-2
| 7 |
�������������˶����ۺ��⣬�漰�����붯�ߣ����ӶȽϸߣ��ѶȽϴڣ�2�����У�ע�����������ȫ����Ҫ��©���ڣ�3�����У���������ȫ�������μ����ɶ���������߶�֮��Ĺ�ϵʽ������г�������⣮�����������ϴ���Ҫ������㣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
ʹ�ö���ʽa2+b2-2ab-1��ֵΪ���������д�ɣ�������
| A��a-b=��1 |
| B��a��b=1 |
| C��a+b=��1 |
| D��a��b=-1 |
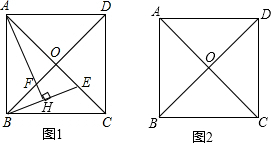 ��ͼ����֪������ABCD��AC��BD�ཻ�ڵ�O��EΪAC��һ�㣬AH��EB��EB�ڵ�H��AH��BD�ڵ�F��
��ͼ����֪������ABCD��AC��BD�ཻ�ڵ�O��EΪAC��һ�㣬AH��EB��EB�ڵ�H��AH��BD�ڵ�F�� ��ͼ��ֱ��y=kx-2��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B����ֱ��AB�ϵĵ�C�ڵ������ޣ���S��BOC=3�����C�����꣮
��ͼ��ֱ��y=kx-2��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B����ֱ��AB�ϵĵ�C�ڵ������ޣ���S��BOC=3�����C�����꣮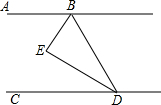 ��ͼ����֪��BEƽ�֡�ABD��DEƽ�֡�BDC���ҡ�EBD+��EDB=90�㣮
��ͼ����֪��BEƽ�֡�ABD��DEƽ�֡�BDC���ҡ�EBD+��EDB=90�㣮