题目内容
16.如图,已知∠MON=90°,点A,B分别在射线MO,ON上,BE是∠ABN的平分线,射线BE的反向延长线与∠BAO的角平分线AC相交于点C.(1)如图1,当∠BAO=70°时,∠ABC是多少度?
(2)当点A,B分别在射线OM,ON上移动时,试问∠ACB的大小是否发生变化?如果不变,请求出∠ACB的度数;如果∠ACB的大小随点A,B的移动而发生变化,请求出∠ACB的度数的变化范围.
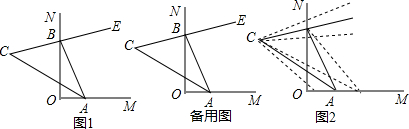
分析 (1)根据角平分线的定义可得:$∠NBE=\frac{1}{2}$∠NBA,然后根据对顶角相等可得:∠CBO=∠NBE,然后由三角形内角和定理可得:∠ABO=20°然后由三角形外角的性质可得:∠NBA=∠MON+∠BAO=160°,进而可得:∠CBO=∠NBE=$\frac{1}{2}$∠NBA=80°,然后由∠ABC=∠CBO+∠ABO即可求出答案;
(2)∠ACB的大小不随点A,B的移动而发生变化,根据三角形的一个外角等于和它不相邻的两个内角的和,∠ABN=∠OAB+∠MON,∠DBA=∠ACB+∠CAB,再根据角平分线的定义∠CAB=$\frac{1}{2}$∠OAB,∠DBA=$\frac{1}{2}$∠ABN,代入整理即可得到∠ACB=$\frac{1}{2}$∠MON=45°.
解答 解:(1)∵BE是∠ABN的平分线,
∴$∠NBE=\frac{1}{2}$∠NBA,
∵∠CBO=∠NBE,
∴∠CBO=$\frac{1}{2}∠NBA$,
∵∠MON+∠BAO+∠ABO=180°,∠MON=90°,∠BAO=70°,
∴∠ABO=20°,
∵∠NBA=∠MON+∠BAO=160°,
∴∠CBO=$\frac{1}{2}$∠NBA=80°,
∴∠ABC=∠CBO+∠ABO=80°+20°=100°;
(2)∠ACB的大小保持不变.理由:
∵∠ABN=90°+∠OAB,AC平分∠OAB,BE平分∠ABN,
∴∠ABE=$\frac{1}{2}$∠ABN=$\frac{1}{2}$(90°+∠OAB)=45°+$\frac{1}{2}$∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠ACB+∠CAB,
∴∠ACB=45°,
故∠ACB的大小不发生变化,且始终保持45°.
点评 本题考查的是三角形内角与外角的关系,解答此题目要注意:
①求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
②三角形的外角通常情况下是转化为内角来解决.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{22}{7}$ | B. | 2-2 | C. | $5.\stackrel{•}1\stackrel{•}5$ | D. | cos45° |
 如图,直线AB、CD交于点O,OE⊥AB,若∠EOD=48°,则∠AOC=42°.
如图,直线AB、CD交于点O,OE⊥AB,若∠EOD=48°,则∠AOC=42°.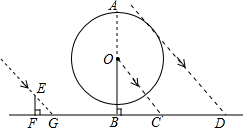 同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.
同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高. 如图是跷跷板的示意图,立柱OC与地面垂直.以O为横板AB的中点,AB绕点O上下转动,横板AB的B端最大高度h是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB=2m,OC=0.5m,通过计算得到此时的h1,再将横板AB换成横板A′B′,O为横板A′B′的中点,且A′B′=3m,此时B′点的最大高度为h2,由此得到h1与h2的大小关系是:h1=h2(填“>”、“=”或“<”).可进一步得出h随横板的长度的变化为不变(填“不变”或“改变”)
如图是跷跷板的示意图,立柱OC与地面垂直.以O为横板AB的中点,AB绕点O上下转动,横板AB的B端最大高度h是否会随横板长度的变化而变化呢?一位同学做了如下研究:他先设AB=2m,OC=0.5m,通过计算得到此时的h1,再将横板AB换成横板A′B′,O为横板A′B′的中点,且A′B′=3m,此时B′点的最大高度为h2,由此得到h1与h2的大小关系是:h1=h2(填“>”、“=”或“<”).可进一步得出h随横板的长度的变化为不变(填“不变”或“改变”)