题目内容
1.先化简,再求值($\frac{{x}^{2}}{{x}^{2}-9}$-$\frac{x+1}{x+3}$)÷$\frac{1}{x-3}$,其中x=$\sqrt{3}$-3.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=[$\frac{{x}^{2}}{(x+3)(x-3)}$-$\frac{(x+1)(x-3)}{(x+3)(x-3)}$]•(x-3)
=$\frac{{x}^{2}-{x}^{2}+2x+3}{(x+3)(x-3)}$•(x-3)
=$\frac{2x+3}{x+3}$,
当x=$\sqrt{3}$-3时,原式=$\frac{2(\sqrt{3}-3)+3}{\sqrt{3}-3+3}$=$\frac{2\sqrt{3}-3}{\sqrt{3}}$=2-$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.一个圆锥的底面半径为8cm,其侧面展开图的圆心角为240°,则此圆锥的侧面积为( )
| A. | 96πcm2 | B. | 48πcm2 | C. | 36πcm2 | D. | 24πcm2 |
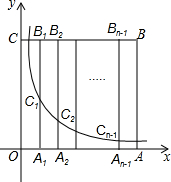 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=$\frac{1}{x}$(x>0)于点C1,C2,…,Cn-1.BC与双曲线y=$\frac{1}{x}$交于点E,若$\frac{{B}_{n-1}E}{{B}_{n-1}{C}_{n-1}}$=$\frac{14}{15}$,则n的值为15.(n为正整数)
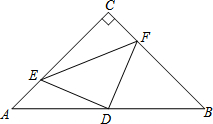 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有①③.(填写所有正确结论的序号)