题目内容
数轴上从左到右等距离排列着点A1、A2、A3…A2013共2013个整数点,它们表示的整数分别记作a1、a2、a3、…a2013为连续整数.
(1)求A2013到A1的距离;
(2)已知a15=-18,求a1、a2013的值;
(3)已知a2013=2014,求a1+a2+a3+…+a2013的值.
(1)求A2013到A1的距离;
(2)已知a15=-18,求a1、a2013的值;
(3)已知a2013=2014,求a1+a2+a3+…+a2013的值.
考点:规律型:数字的变化类,数轴
专题:
分析:(1)根据题目提供的两点间的距离公式进行计算;
(2)逆用两点间的距离公式计算即可得解.
(3)把a1+a2+a3+…+a2013=2+3+4+…+2014求解即可.
(2)逆用两点间的距离公式计算即可得解.
(3)把a1+a2+a3+…+a2013=2+3+4+…+2014求解即可.
解答:解:(1)∵a2=a1+1,a3=a2+1=a1+2…、a2013=a1+2012,a2013>a1,
∴|A2013A1|=|a2013-a1|=a2013-a1=a1+2012-a1=2012;
(2)∵a15=a1+14,
∴a1=a15-14=-18-14=-32;
a2013=a1+2012=1980.
(3)a1+a2+a3+…+a2013=a2013-2012+a2013-2011+…a2013=2+3+4+…+2014=
=2029104.
∴|A2013A1|=|a2013-a1|=a2013-a1=a1+2012-a1=2012;
(2)∵a15=a1+14,
∴a1=a15-14=-18-14=-32;
a2013=a1+2012=1980.
(3)a1+a2+a3+…+a2013=a2013-2012+a2013-2011+…a2013=2+3+4+…+2014=
| (2+2014)×2013 |
| 2 |
点评:本题考查了数轴及数字的变化类,读懂题目信息,明确两点之间的距离公式是解题的关键.

练习册系列答案
相关题目
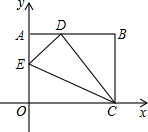 如图,将一矩形纸片OABC放在直角坐标系中,O为原点,C在x的正半轴上,OA=6,OC=10,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标.
如图,将一矩形纸片OABC放在直角坐标系中,O为原点,C在x的正半轴上,OA=6,OC=10,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标.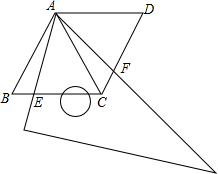 用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,如果使三角尺60°角的顶点与点A重合,两边分别与AB、AC重合,将三角尺绕A点按逆时针方向旋转.如图,三角尺的两边分别与菱形的两边BC、CD相交于点E、F.
用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,如果使三角尺60°角的顶点与点A重合,两边分别与AB、AC重合,将三角尺绕A点按逆时针方向旋转.如图,三角尺的两边分别与菱形的两边BC、CD相交于点E、F.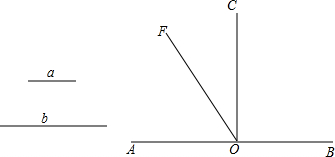
 如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条?
如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条? “勾股定理”是指在直角三角形中,两条直边的平方和等于斜边的平方,例如:一个直角三角形的两条直角边分别为3和4,那么有:32+42=52,即斜边的长为5.已知图中两条直角边的长度,求以斜边长为直径的圆的面积.
“勾股定理”是指在直角三角形中,两条直边的平方和等于斜边的平方,例如:一个直角三角形的两条直角边分别为3和4,那么有:32+42=52,即斜边的长为5.已知图中两条直角边的长度,求以斜边长为直径的圆的面积.