题目内容
(本题满分12分)
如图,在△ 中,∠
中,∠ >∠
>∠ ,
, ,
,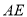 平分∠
平分∠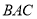 .
.
(1)若∠ =70°,∠
=70°,∠ =30°.
=30°.
①求∠ = °;②∠
= °;②∠ = °.
= °.
(2)探究:小明认为如果只要知道∠ -∠
-∠ =n°,就能求出∠
=n°,就能求出∠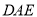 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | |
50° | 20° | |
80° | 56° |
②结论:当 时,试用含
时,试用含 的代数式表示∠
的代数式表示∠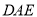 的度数,并写出推导过程;
的度数,并写出推导过程;
③应用:若∠ =56°,∠
=56°,∠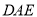 =12°,则∠
=12°,则∠ = °.
= °.

(1)①40°;②20°;(2)①填表详见解析;②∠DAE=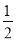 n°;③ 74°.
n°;③ 74°.
【解析】
试题分析:(1)①利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAE;
②先求出∠BAD,就可知道∠DAE的度数;
(2)①②用∠B,∠C表示∠DAE,进一步计算,并验证结论即即可;
③利用结论得出∠B-∠C,利用三角形的内角和得出∠B+∠C,进一步求得答案即可.
试题解析:(1)①∵∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=40°;
②∵AD⊥BC,∠B=70°,
∴∠BAD=90°-∠B=90°-70°=20°,
而∠BAE=40°,
∴∠DAE=20°;
故答案为:①40°;②20°;
(2)①填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | 20° |
50° | 20° | 15° |
80° | 56° | 12° |
②解:在△ABC中,∠BAC=180°-∠B-∠C.
∵AE平分∠BAC,
∴∠BAE=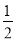 ∠BAC=
∠BAC=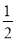 (18O°-∠B-∠C)=90°-
(18O°-∠B-∠C)=90°-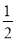 ∠B-
∠B-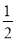 ∠C,
∠C,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD+∠B=90°,
∴ ∠BAD=90°-∠B,
∴ ∠DAE=∠BAE-∠BAD=(90°-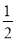 ∠B-
∠B-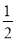 ∠C)-(90°-∠B)=
∠C)-(90°-∠B)=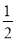 ∠B-
∠B-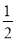 ∠C=
∠C=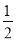 (∠B-∠C)=
(∠B-∠C)=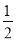 n°;
n°;
③∵∠A=56°,
∴∠B+∠C=124°,
∵∠DAE=12°,
∴∠B-∠C=24°,
∴2∠B=148°,
∴∠B=74°.
故答案为:74°.
考点:角平分线的定义;三角形的内角和定理.

 的度数
的度数 的度数
的度数 的度数
的度数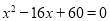 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( ) D.
D.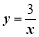 B.
B. C.
C. D.
D.
 ,则扇形OAB的面积是 .
,则扇形OAB的面积是 .
 三边的中点,下列说法正确的是( )
三边的中点,下列说法正确的是( ) 的面积之比为2:1
的面积之比为2:1 
 与3互为倒数,则
与3互为倒数,则 的值为 .
的值为 .
