题目内容
(本题满分12分)甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.

(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数表达式,并写出相应的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
(1)40;
(2) ;
;
(3)甲车行驶1小时(或1-1.5小时)或 小时或
小时或 小时,两车恰好相距40km.
小时,两车恰好相距40km.
【解析】
试题分析:(1)根据“路程÷时间=速度”由函数图象就可以求出甲的速度求出a的值;
(2)由分段函数当0≤x≤1,1<x≤1.5,1.5<x≤7由待定系数法就可以求出结论;
(3)先求出乙车行驶的路程y与时间x之间的解析式,由解析式之间的关系建立方程求出其解即可.
试题解析:【解析】
(1)由题意 ,
,
所以 ;
;
(2)当 时,设y与x之间的函数关系式为
时,设y与x之间的函数关系式为 ,
,
把(1,40)代入,得 ,
,
∴ ,
,
当 时
时 ;
;
当 设y与x之间的函数关系式为
设y与x之间的函数关系式为 ,
,
由题意得: ,解得
,解得 ,
,
∴ ,
,
∴ ;
;
(3)设乙车行驶的路程y与时间x之间的解析式为 ,
,
由题意得: ,解得
,解得 ,
,
∴ ,
,
当40x﹣20﹣(80x﹣160)=40时,
解得:x= .
.
当80x﹣160-(40x﹣20)=40时,
解得:x= .
.
答:甲车行驶1小时(或1-1.5小时)或 小时或
小时或 小时,两车恰好相距40km.
小时,两车恰好相距40km.
考点:待定系数法求一次函数解析式;一次函数与一元一次方程的关系.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案(本题满分12分)
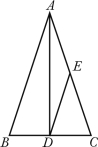
如图,在△ 中,∠
中,∠ >∠
>∠ ,
, ,
,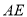 平分∠
平分∠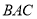 .
.
(1)若∠ =70°,∠
=70°,∠ =30°.
=30°.
①求∠ = °;②∠
= °;②∠ = °.
= °.
(2)探究:小明认为如果只要知道∠ -∠
-∠ =n°,就能求出∠
=n°,就能求出∠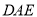 的度数?请你就这个问题展开探究:
的度数?请你就这个问题展开探究:
①实验:填表
∠ | ∠ | ∠ |
70° | 30° | (此格不需填写) |
65° | 25° | |
50° | 20° | |
80° | 56° |
②结论:当 时,试用含
时,试用含 的代数式表示∠
的代数式表示∠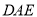 的度数,并写出推导过程;
的度数,并写出推导过程;
③应用:若∠ =56°,∠
=56°,∠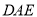 =12°,则∠
=12°,则∠ = °.
= °.

 中,
中, ,
, ,
, 为
为 上一点,
上一点, ,
, ,求
,求 的长.
的长.
 的方程是( ).
的方程是( ). B.
B.
 D.
D.
 )、B(2,
)、B(2, )都在一次函数
)都在一次函数 的图象上,则
的图象上,则 中自变量
中自变量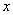 的取值范围是
的取值范围是 C.x≥-3或
C.x≥-3或